静力学

概念

词汇理解

平衡：保持静止或匀速直线运动
平衡力系：力系作用下处于平衡
刚体：大小形状不变
变形体：力的作用下大小形状不变
二力体：只在两个力作用下平衡的刚体
自由体：位移不受限制
非自由体：位移受到限制
约束：对非自由体的某位移预先施加限制条件称为约束
约束力：代表约束的力，方向总是知道的和限制物体位移的方向相反。

基本公理

公理1：力的平行四边形法则

力可以根据向量法则合成

公理2：二力平衡原理

作用于刚体上的两个力，是刚体平衡
大小相等，方向相反，在同一物体共线

公理3：加减平衡力系原理

作用于一刚体上的任一力系，加上或减去任意个平衡力系，不改变原来力系对刚体的作用效应

推论一：力的可传递性原理

某刚体上的力平移，作用效果不变
推论二：三力平衡汇交定理

刚体平衡三个力交与一点

公理4：作用与反作用力

两物体相互作用，大小相等，方向相反，同一直线，分别作用两个物体

公理5：刚化原理

处于平衡状态的变形体，而可用刚体静力学的平衡理论

约束约束反力画法（约束反力简称约束力和反力F_A）

柔性约束：

只能阻止物体向下运动，约束力沿中线背离物体

方向延绳背离物体

光滑面约束：

方向沿公法线

固定铰支座：

限制物体在平面内任意方向的移动，不限制转动，约束反力不确定

方向不确定

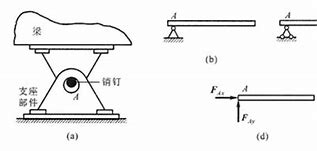
滚动铰链支座：

限制物体平面垂直方向移动，不限制水平

光滑连接铰链：

约束反力不确定，限制垂直，不限制转动

可动铰支座：

只限制物体竖直方向运动

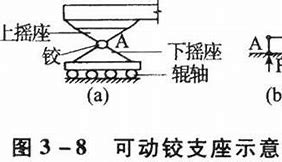
二力杆约束：

只有沿受力点拉力和压力

滑动铰约束：

限制垂直不限水平

固定端约束：

限制各个方向的运动

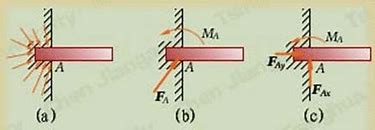
物体受力分析

主动力：重力，风力，气压

被动里：约束力

1.简化结构取脱离体

2.分析受力画主动力

3.简化约束画约束力

4.分析约束反力的方向

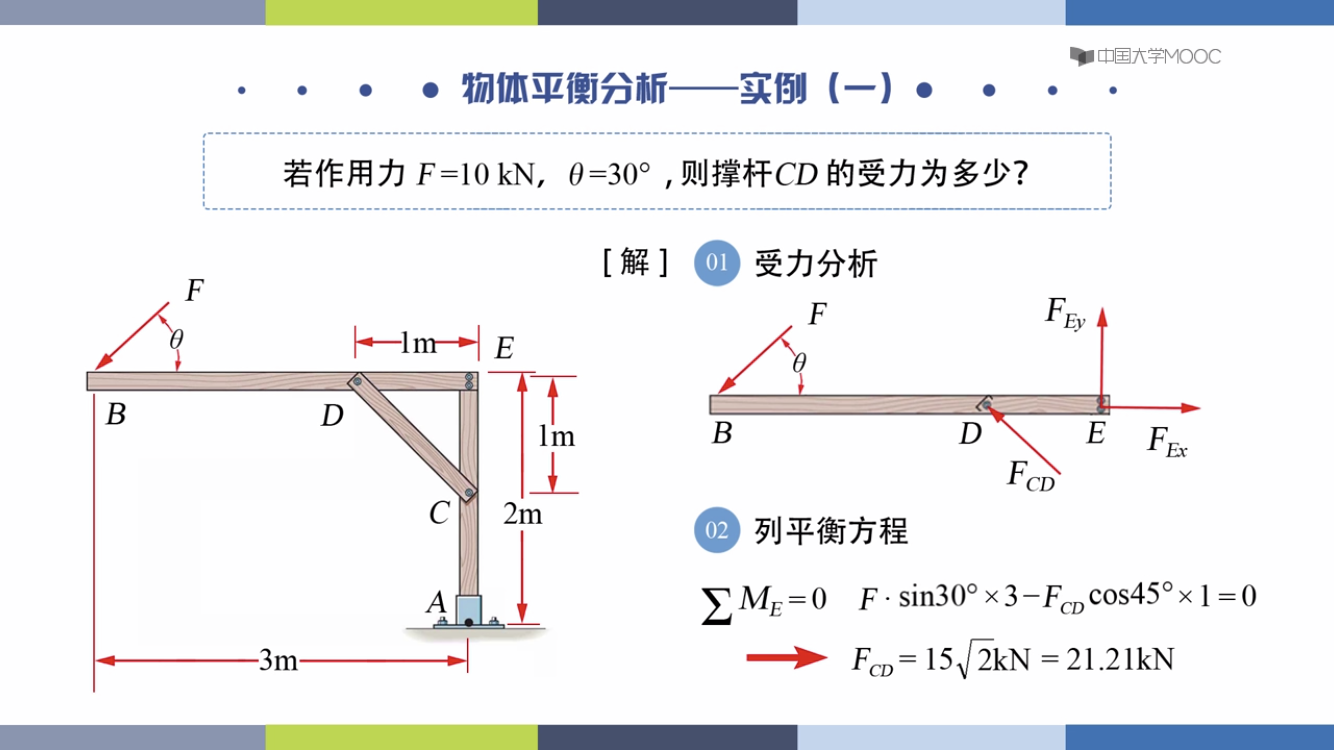
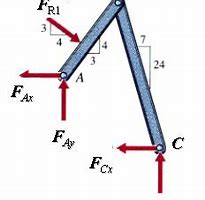
右边是一个二力杆，二力方向相反在一个水平线上，左边有主动力F，三力平衡汇交F^’_c，F_A，F汇交与一点。

整体受力分析不需要画出F^’_c，F_c，因为他们是一对内力。可以把F_A，F_B化成坐标轴方向的力

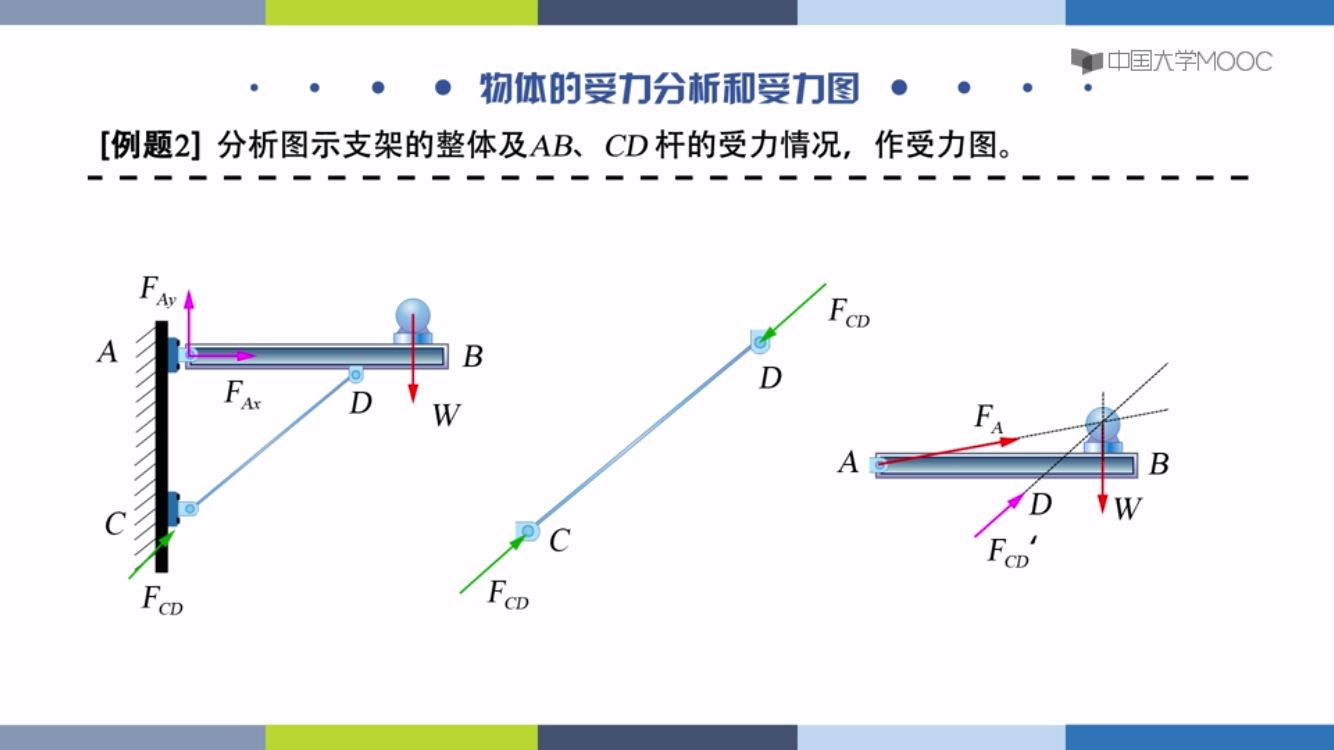
CD是一个二力杆，AB有一个重物的主动力，三力平衡汇交，画出其他两个力，不过我觉得F_A画反方向了。整体受力图同样不画内力

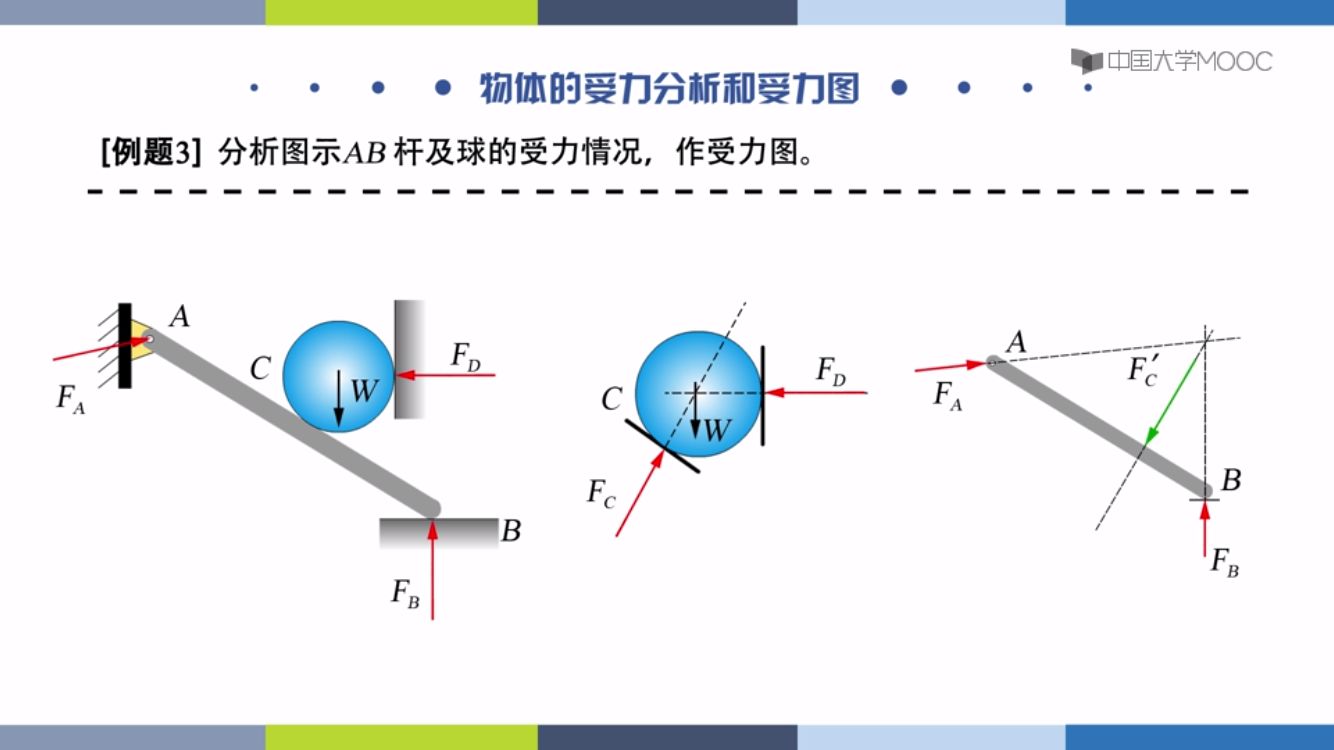
球受两个墙壁的力，AB杆受一个F^’_c他是球的反作用力，三力平衡汇交。整体受力图没有内力。

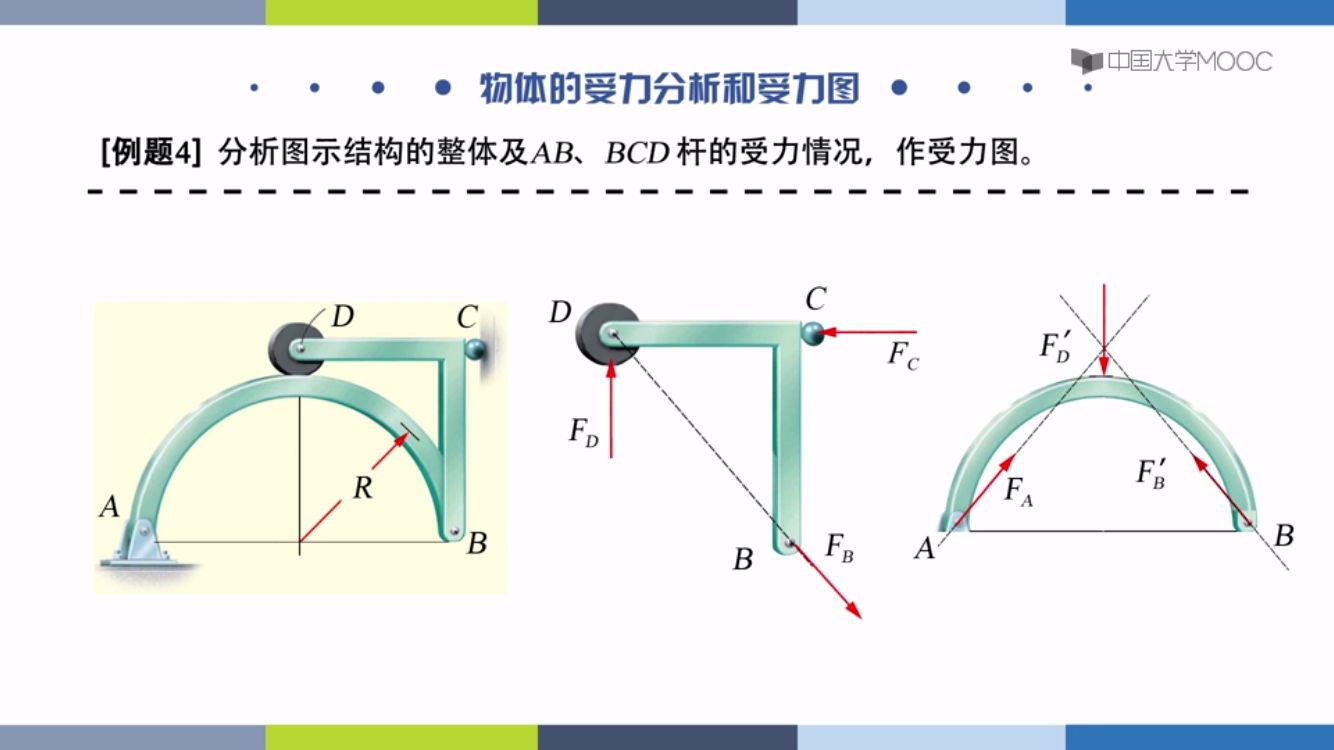
D，C点是光滑面约束，受力都是垂直。三力平衡汇交得到F_B，AB物体受主动力F_B的反作用力F^’_B，三力平衡汇交。

整体受力分析只画A，C端其他都是内力。

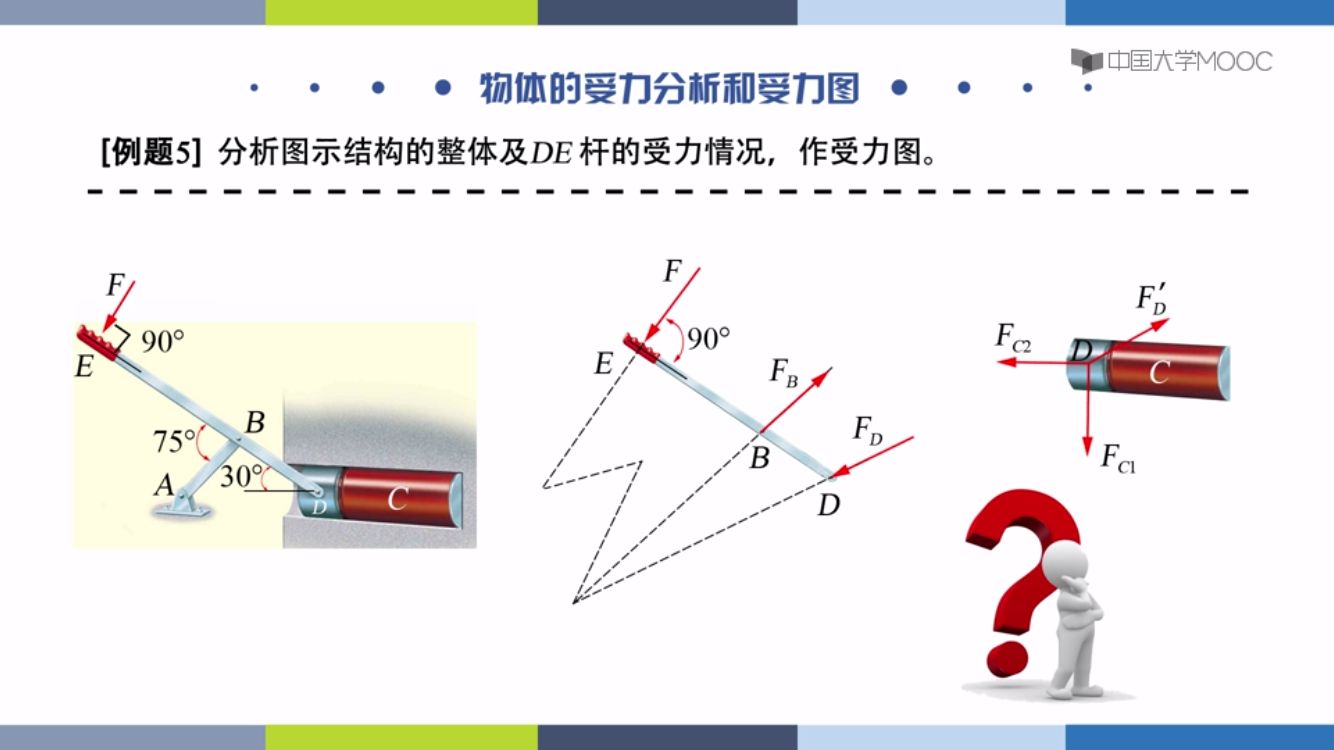
AB杆是二力杆，力的向如F_B所示，知道主动力F,三力平衡汇交。（汇交原理不清楚）

D点有C气体的推力，F_D的反作用力，三力平衡汇交则必有一个力

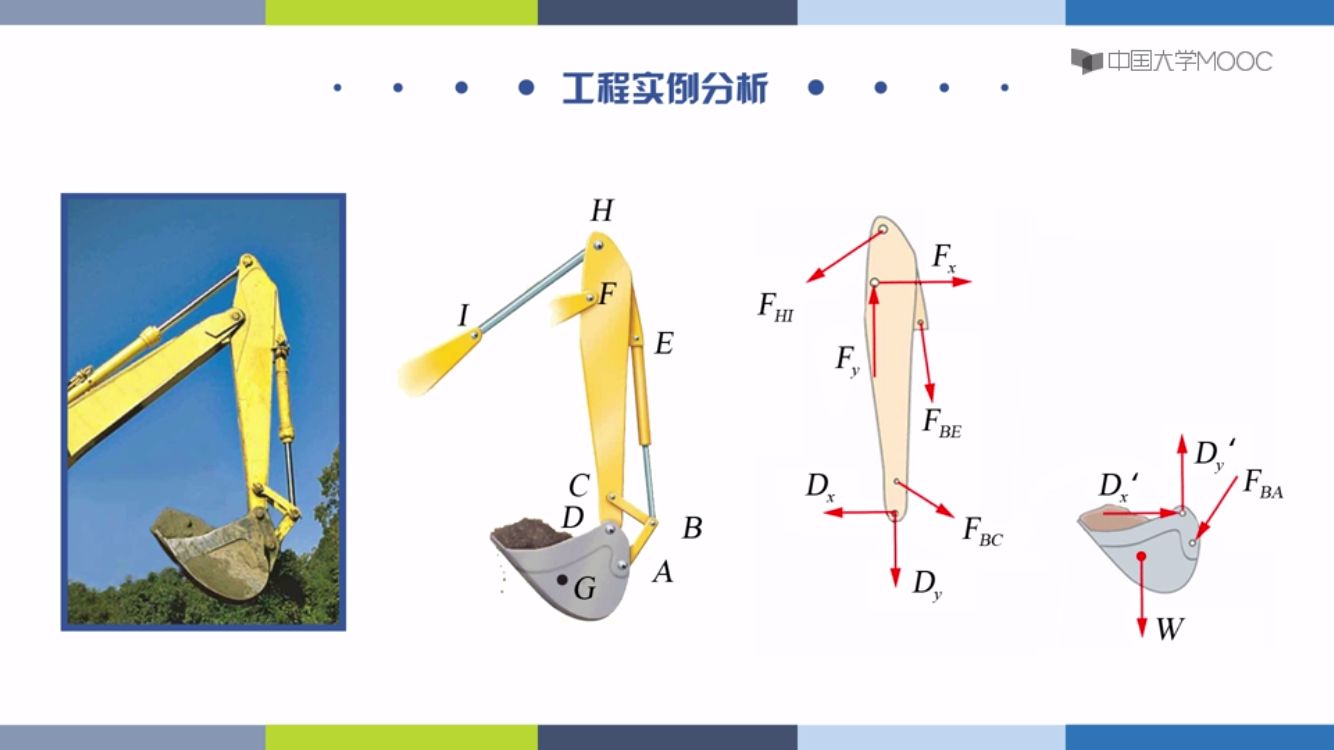
挖掘机的模型。

力矩：力的转动效应

力和力臂的乘积叫力矩N·m

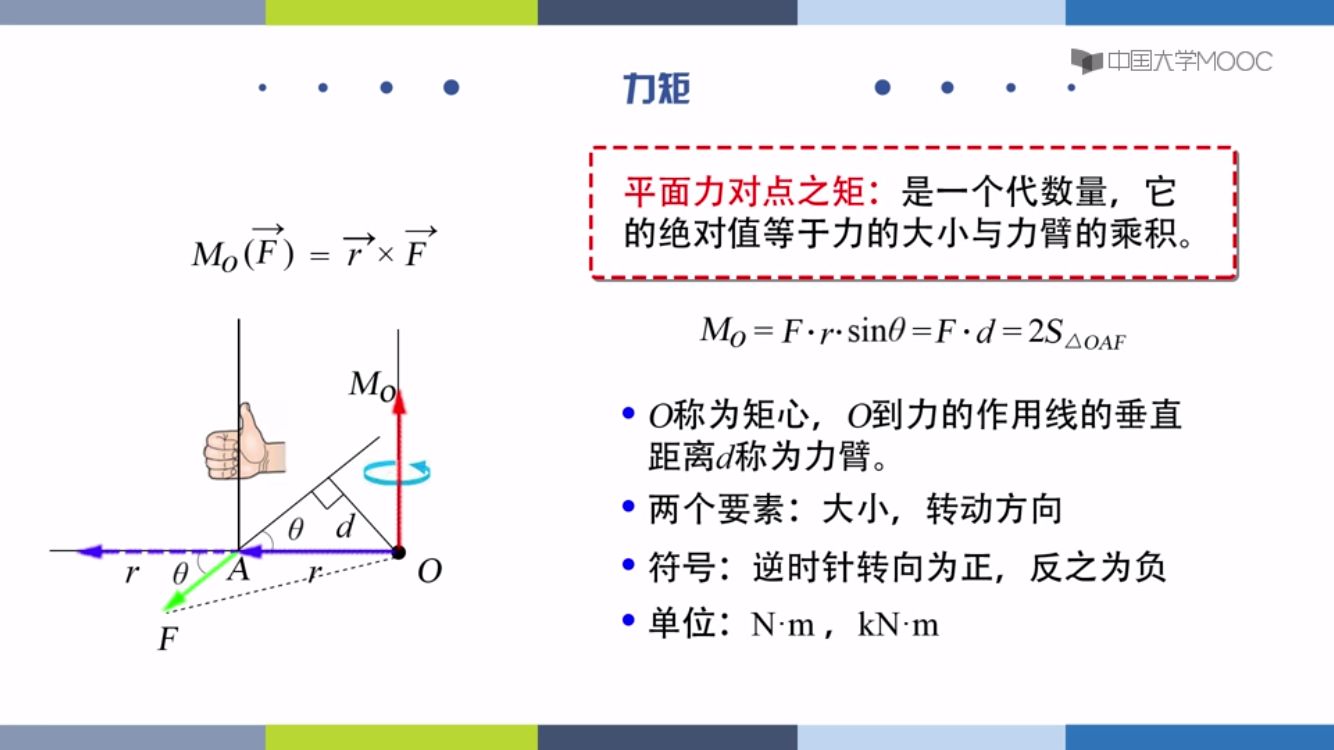
物体转动效应：与力的的大小和轴到作用线距离有关

方向：逆正，顺负

单位：NM

M_o=Fd

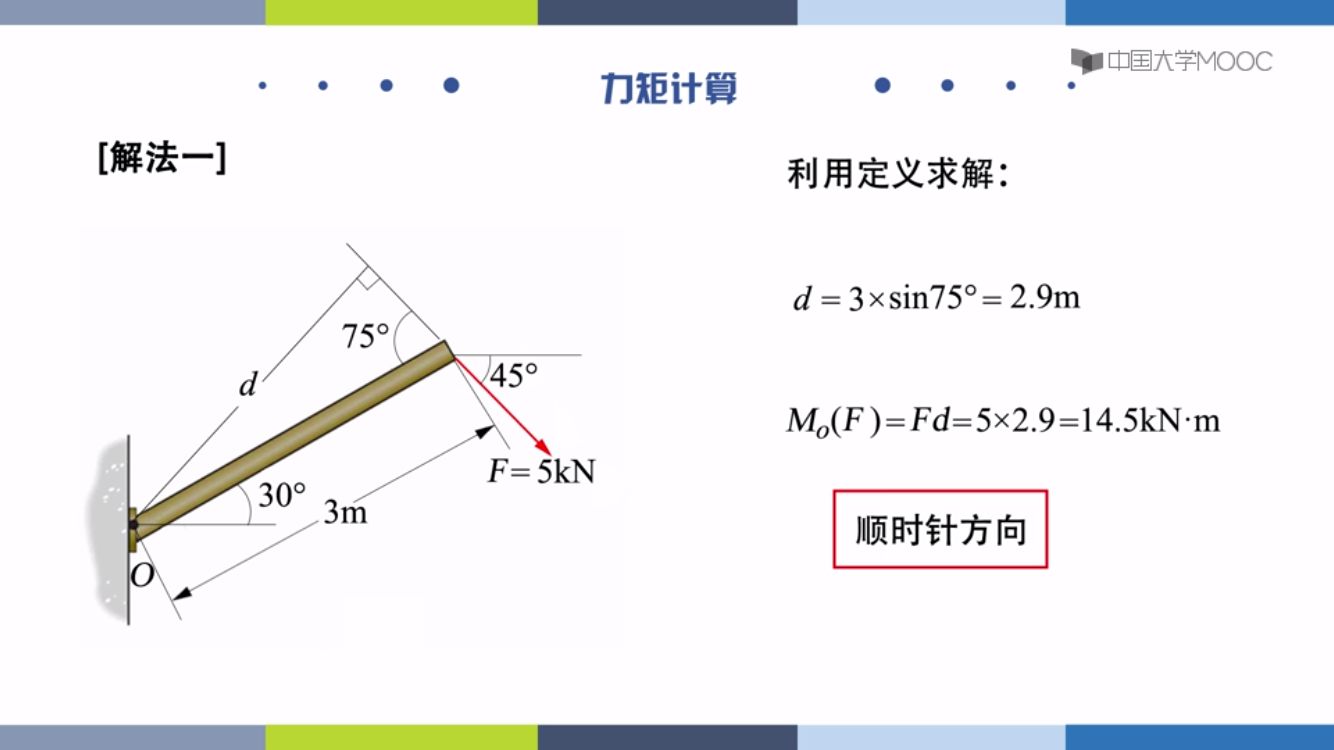
合力矩：合力F对A点的矩等于个分力对A点的矩整合

$Fd=F_1d_1+F_2d_2 \ \ \ \ \ \ \ \ M_A(F)=\Sigma M_A(F_i)$

平行和力矩：

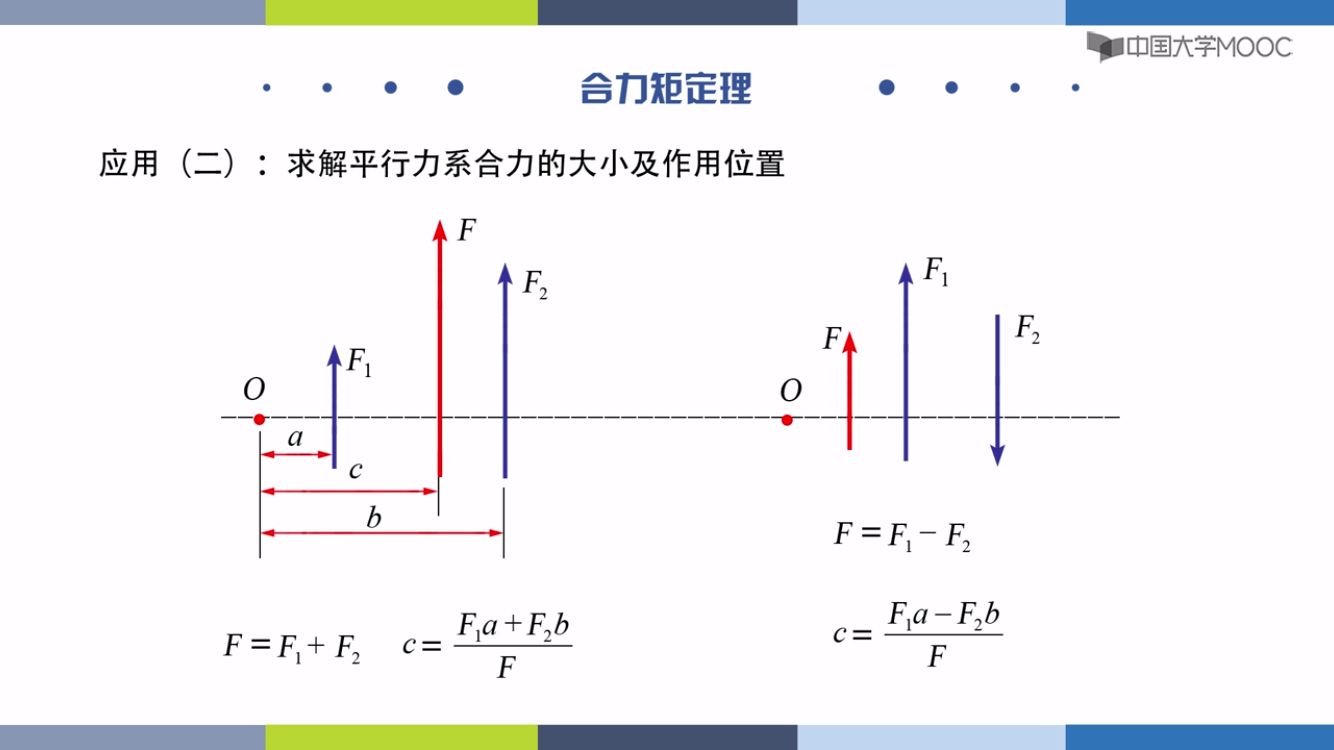
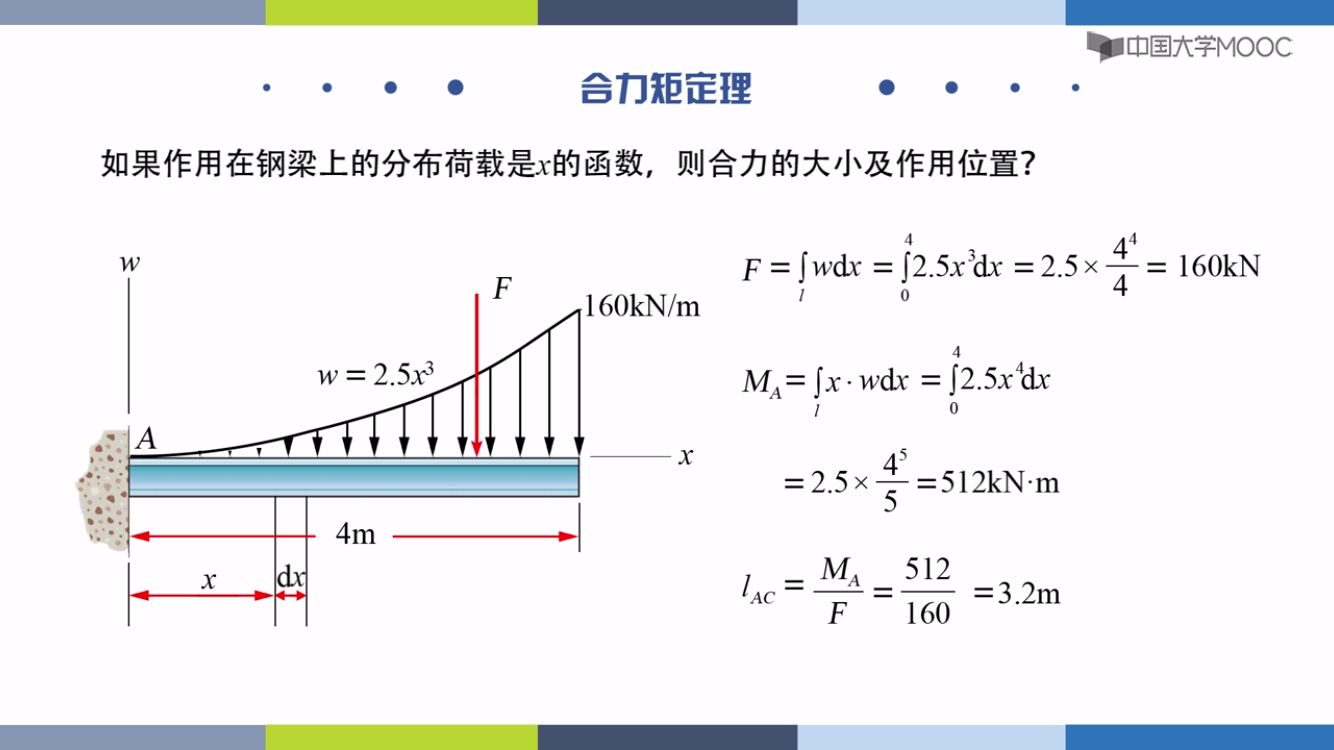
三角形分布荷载

合力距离低端1/3处

梯形分布荷载

分成矩形和三角形，矩形在中间，三角形距低端1/3，再由F=F₁+F₂得到F距离

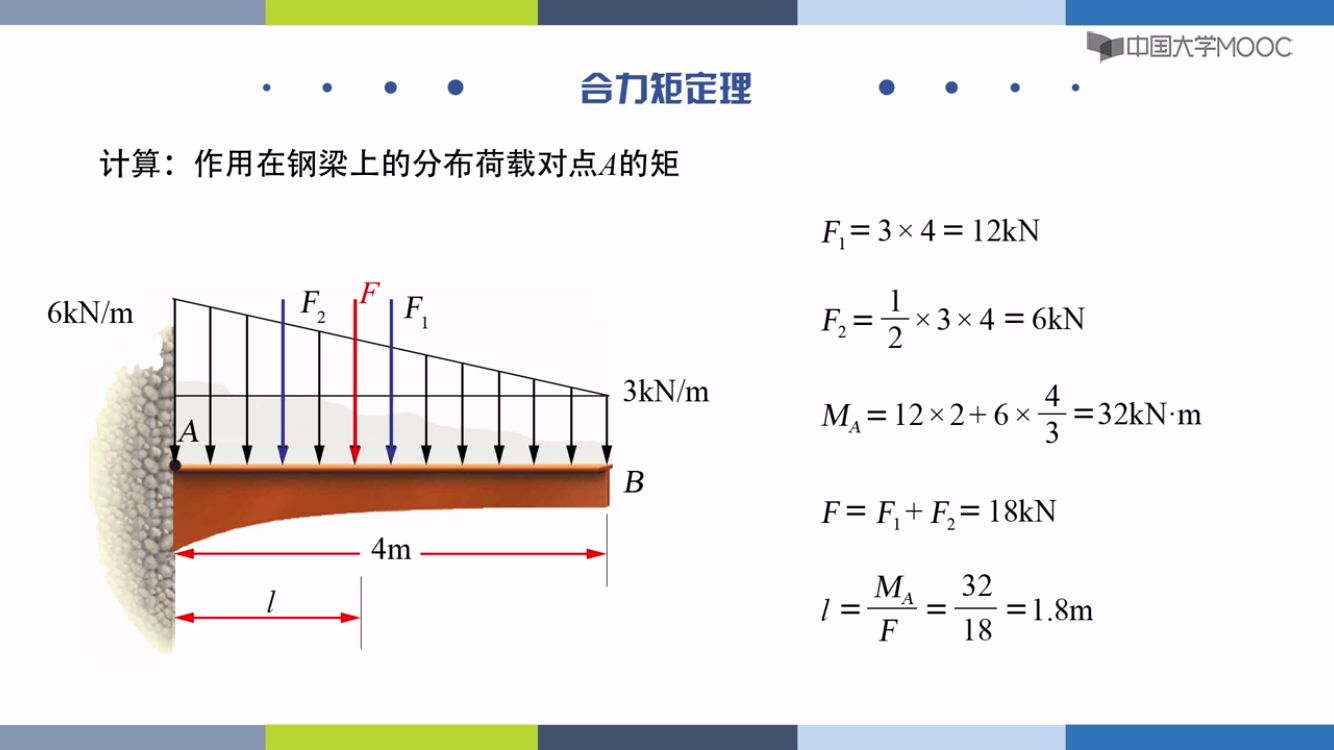
任意分布荷载

积分求解

力偶

力偶距：一个平行力与距离之间的乘积

$M(F,F^,)=\pm Fd$

1.力偶不能用一个力来等效无合力

2.在任意坐标轴上的投影为零

3.不因矩心的改变而改变

4.只要力偶距不变，力偶任意移动作用效果都不变

5.方向逆时针为正顺时针为负

平面力偶系合成结果还是一个力偶，且和力偶矩为各力偶矩的代数和，合力偶等于0则平面力偶系是平衡的。

$M=m_1+m_2+m_3...+m_n$

力系

平面力系：各力作用在同一平面

汇交力系：各力作用汇交一点

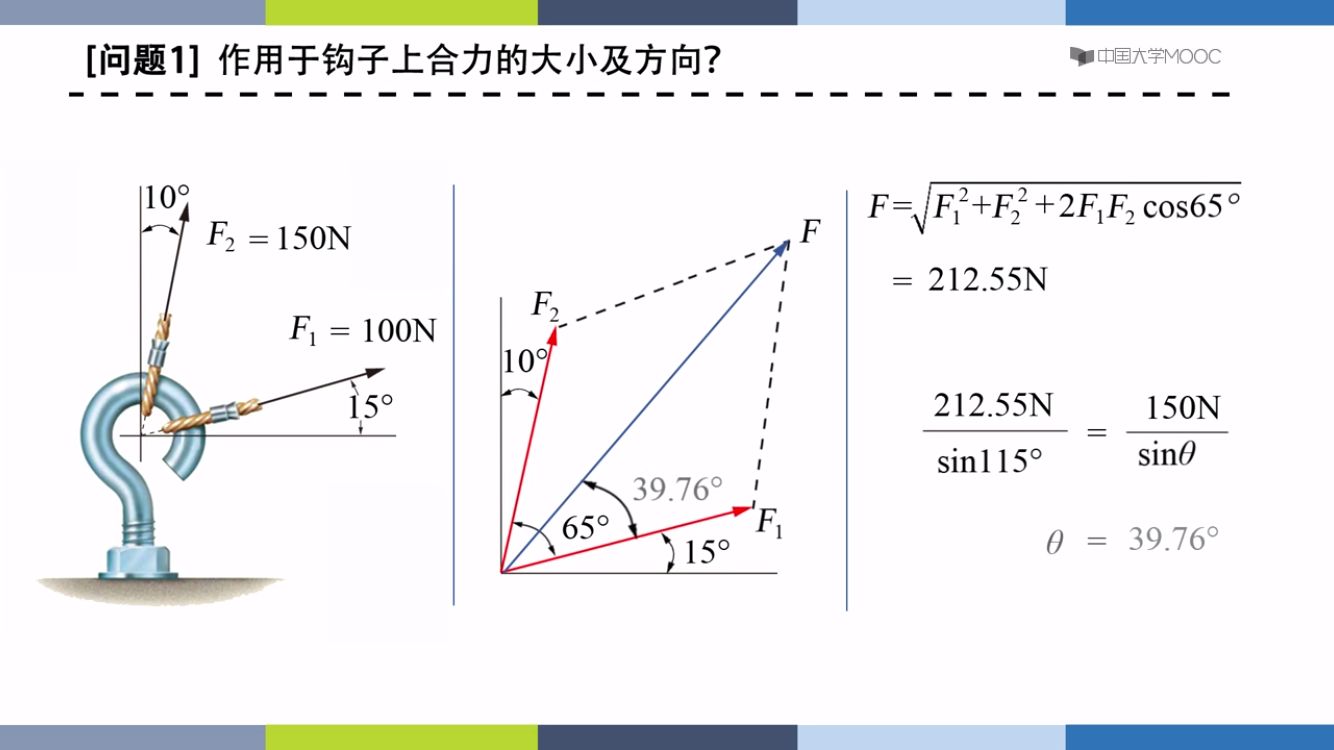
平面汇交力系：

所有力分布在同一平面并汇交与一点

力系矢量求和：求大小

$F=\sqrt{F^2_1+F^2_2+2F_1F_2cos\theta^。}$

正弦函数：求角度

$\frac{F_1}{sin\theta}=\frac{F_2}{sin\theta}$

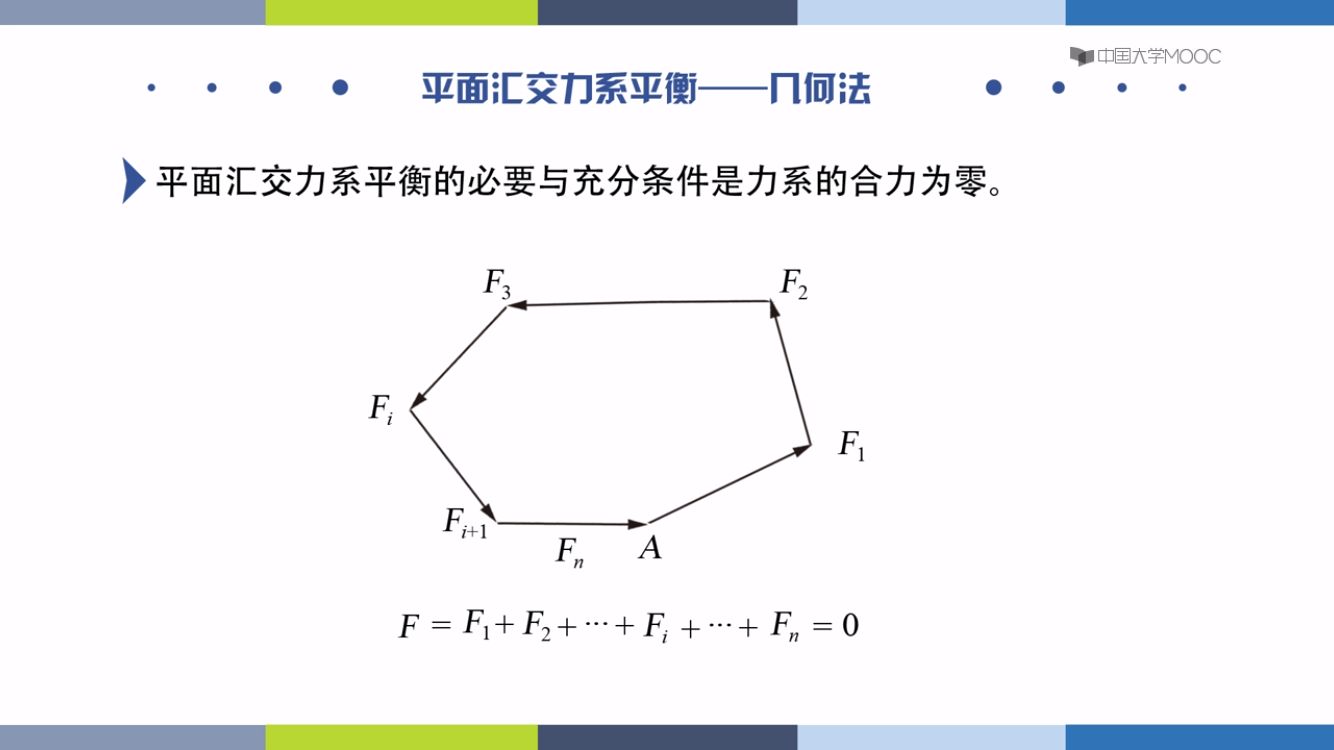
几何法求力系：

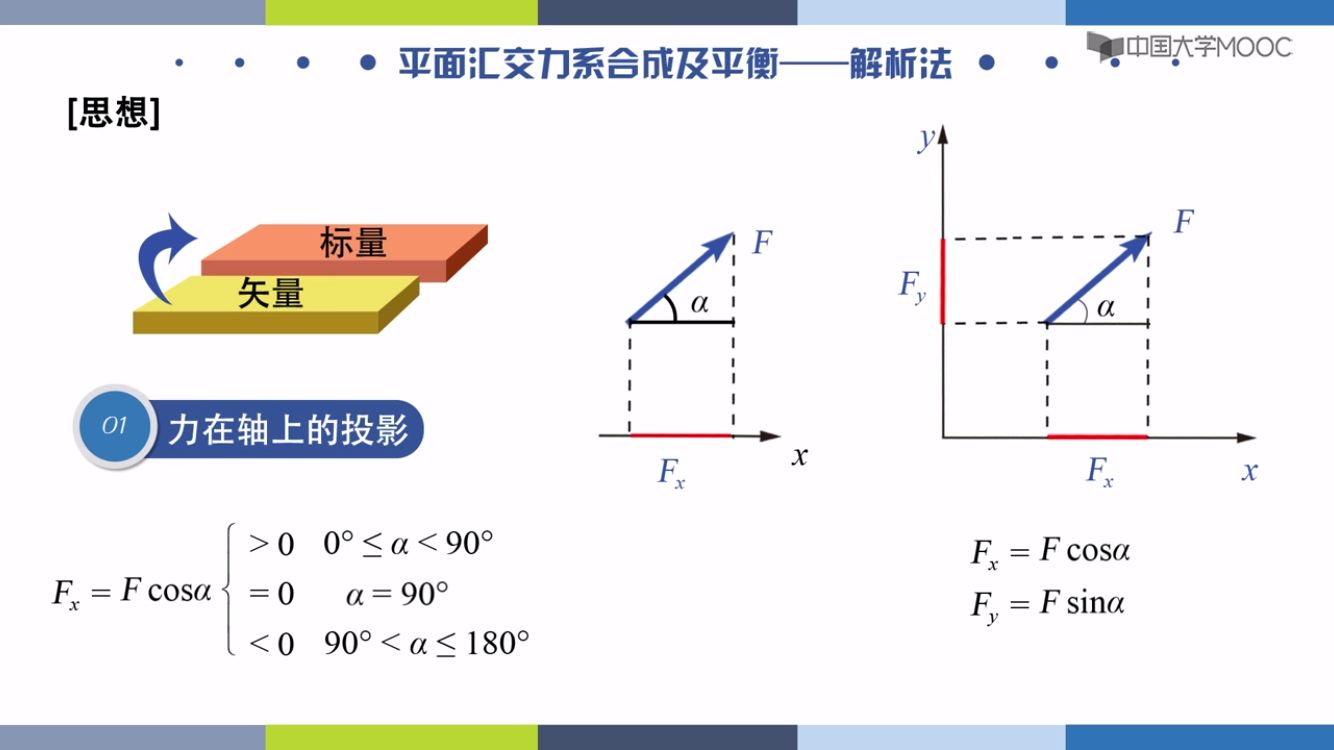
解析法求力系：矢量换成代数量

力在轴上的投影

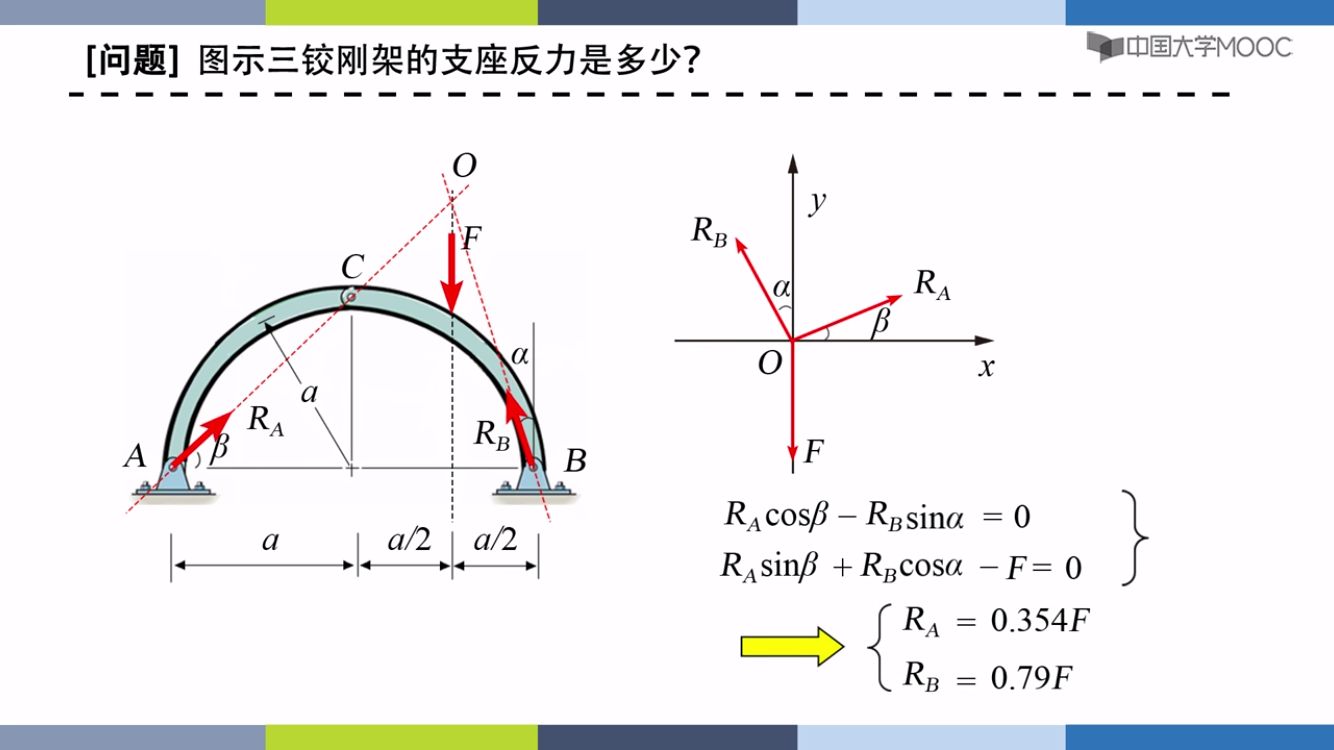
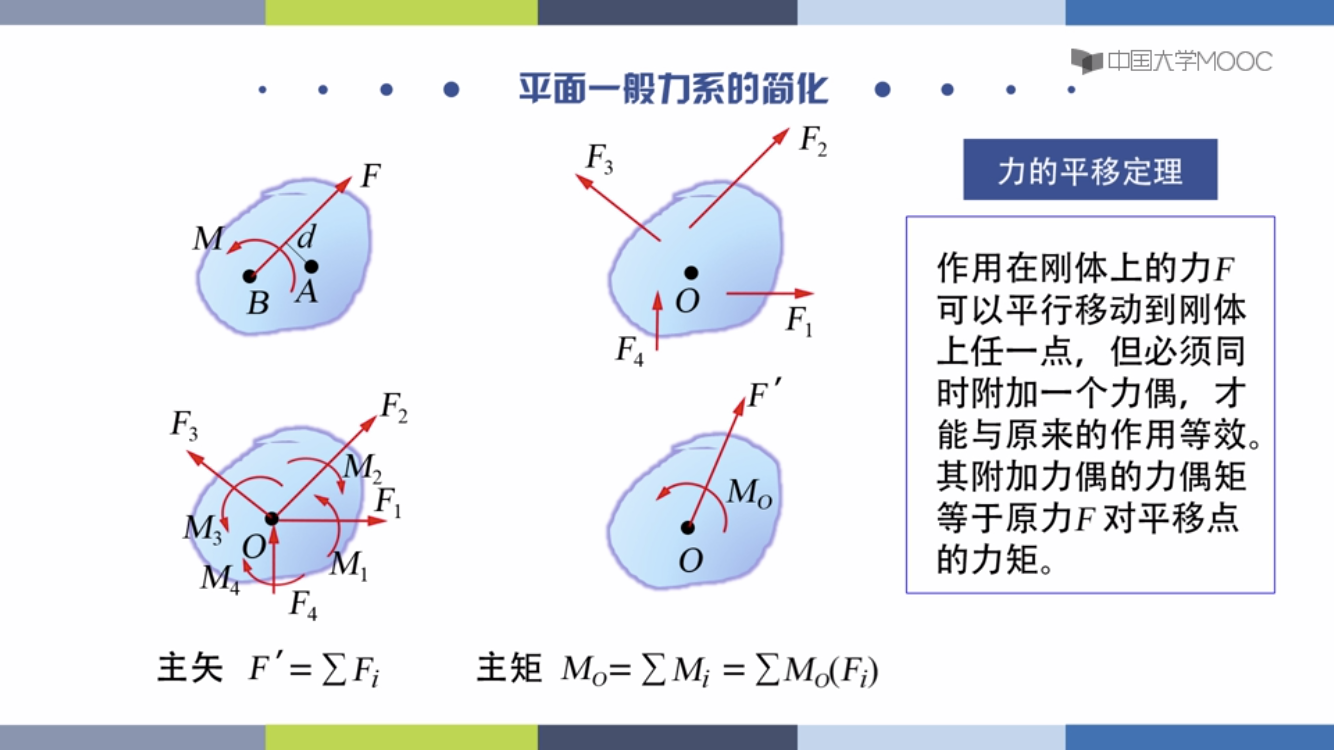
$F_x=Fcos\alpha \\ F_y=Fsin\alpha \\ F=\sqrt{F_x^2+F_y^2}=\sqrt{(\Sigma F_{xi})^2+(\Sigma F_{yi})^2}$

平面一般力系：

各力都在同一平面，且各作用线不汇交于一点，又不相互平行

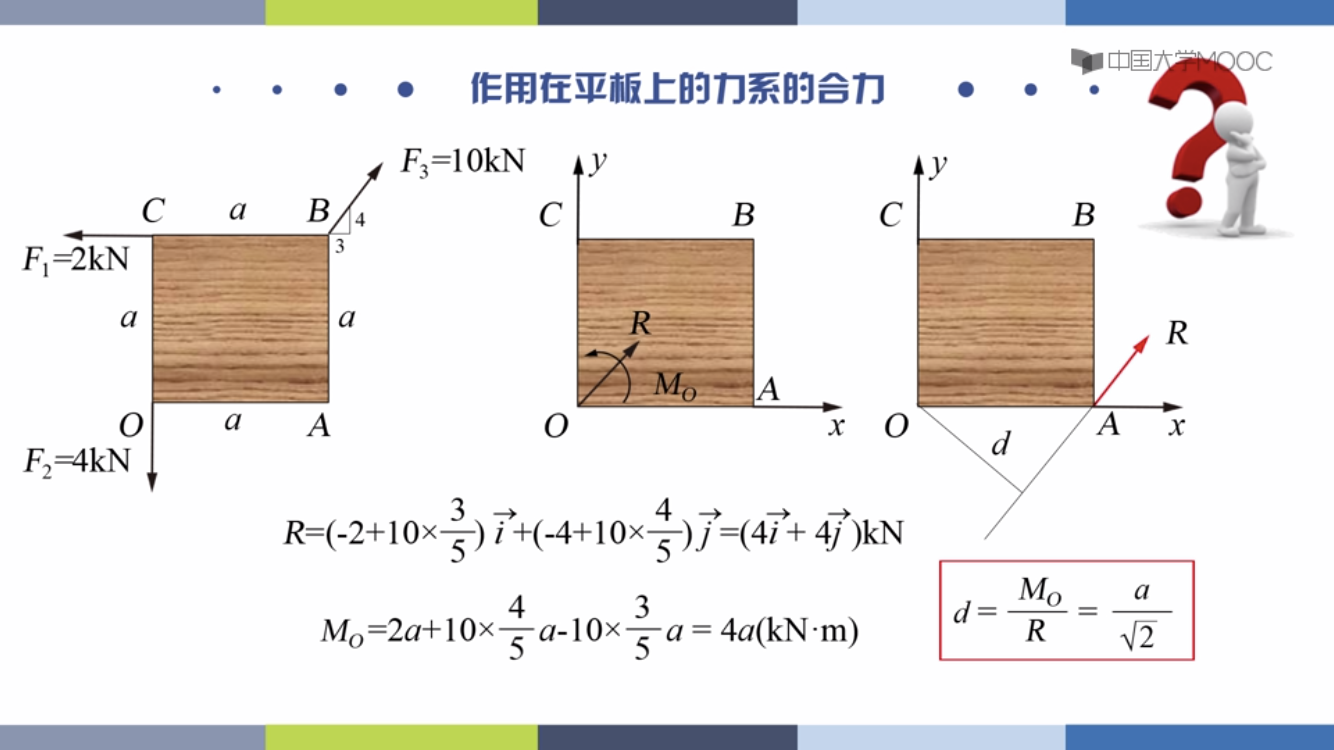
简化：力平移加上一个反向的偶抵消。

主矢：方向力，和是矢量和，和简化中心没关系

主矩：力偶，和是代数和，和简化中心有关系

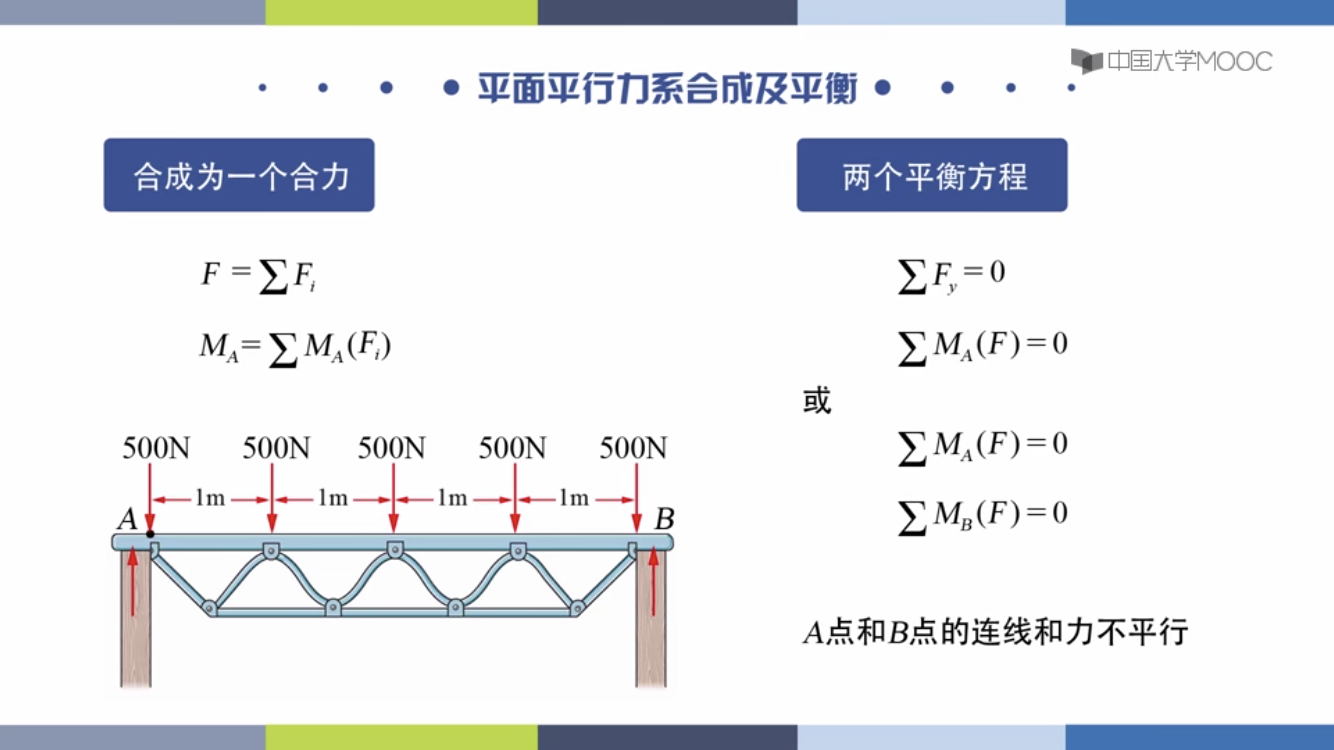
$F^‘=0,M_o\ne 0 \ \ 等效一个力偶，和简化中心无关,性质4 \\ F^‘\ne0,M_o=0 \ \ 等效一个力，和简化中心有关 \\ F^‘\ne0,M_o\ne 0 \ \ 最终简化结果是一个力和一个力偶，进一步简化为一个力\\ F^‘=0,M_o= 0 \ \ 原力系平衡$

平面平行力系

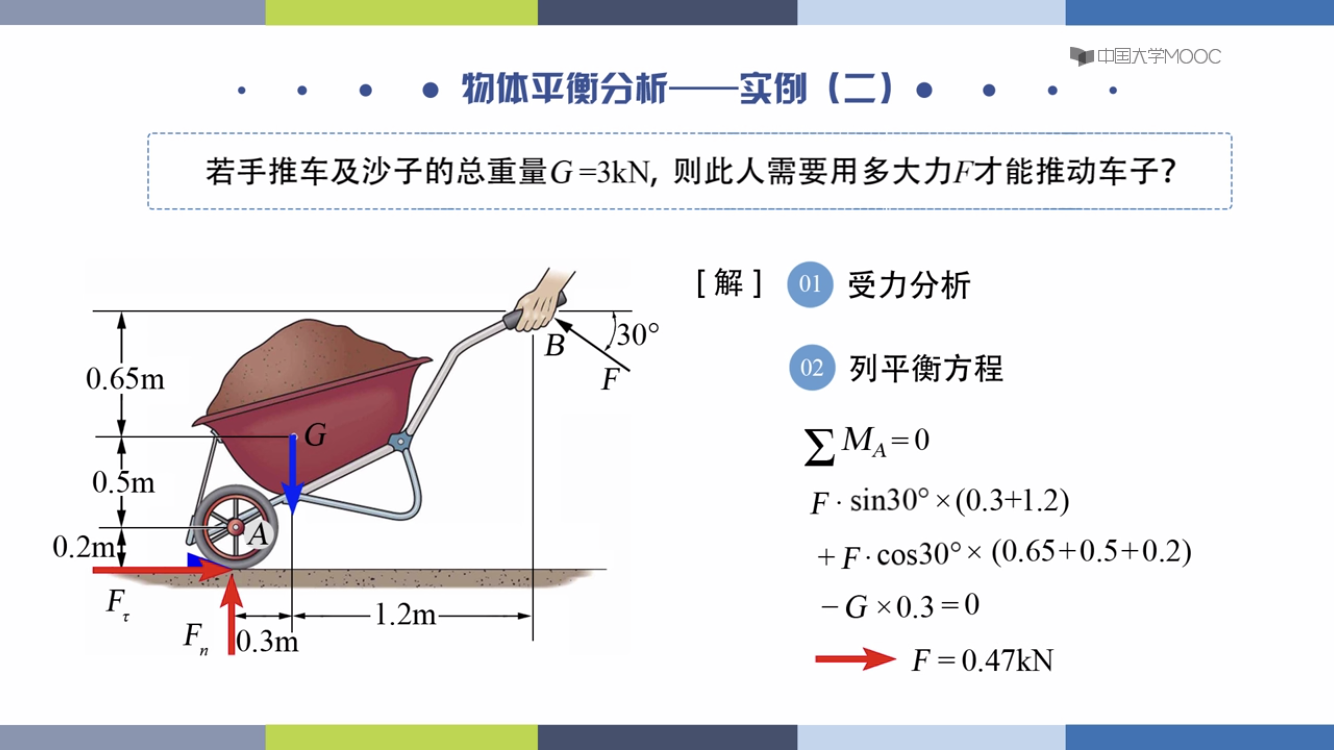
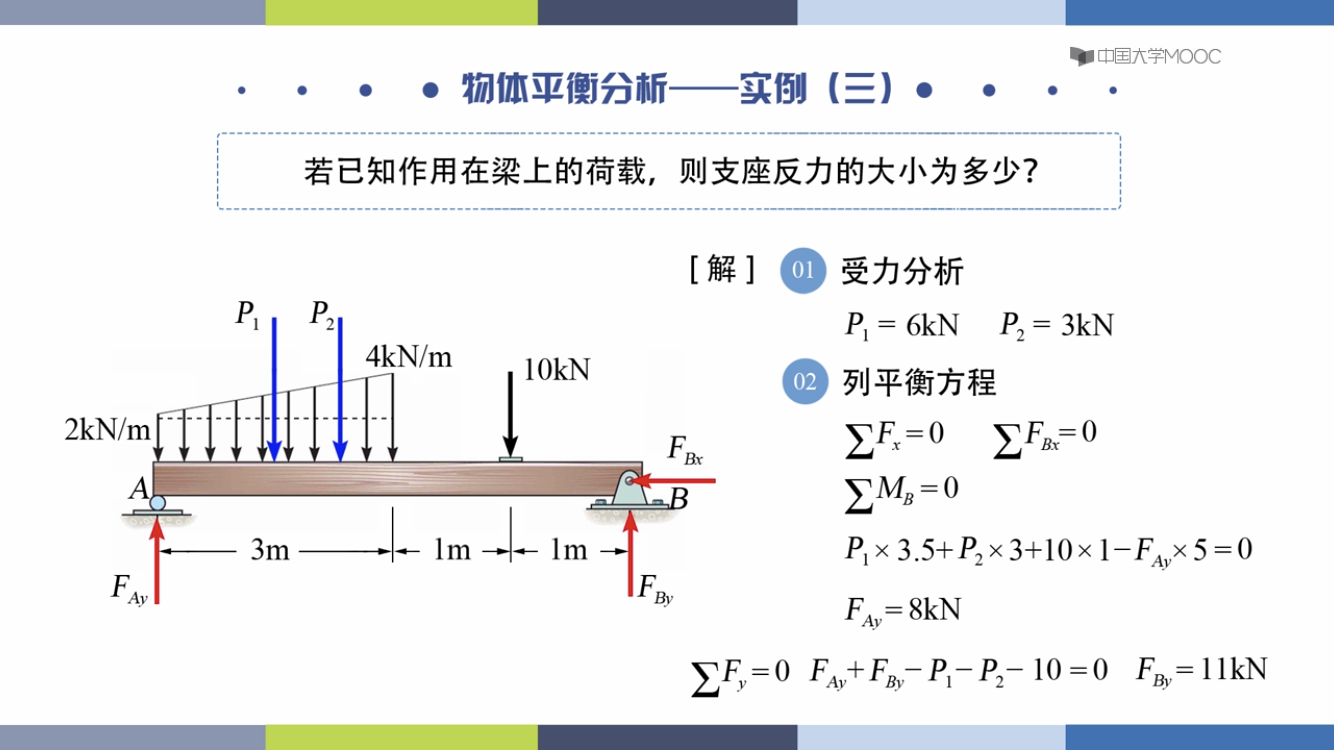
物体平衡分析

最多有三个方程，求三个未知力

$\Sigma M=0 \\ \Sigma F_x=0 \\ \Sigma F_y=0$

例题：

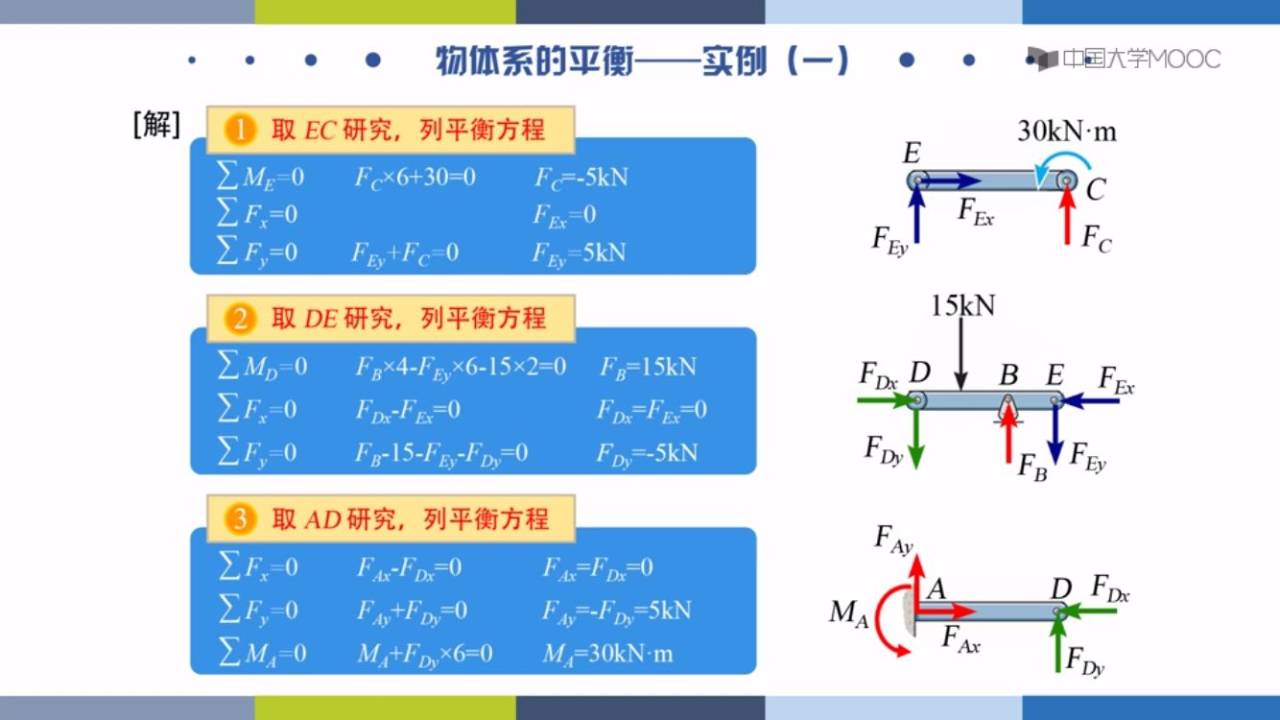
平面平行力系

指仅受垂直某坐标轴的平行力系。

只能列两个方程

\Sigma M=0 \\ \Sigma F_x=0 \ \ or\ \ \Sigma F_y=0

求解力系方法

力系类型	平衡方程	方程个数
共线力系	∑F_x=0	1
平面力偶系	M₀=0	1
平面汇交力系	∑F_x=0，∑F_y=0	2
平面平行力系	∑F_y=0，∑m₀（F）=0	2
平面一般力系一矩式	∑F_x=0，∑F_y=0，∑m₀（F）=0	3
平面一般力系二矩式	∑F_x=0，∑m_A（F）=0，∑m_B（F）=0	3
平面一般力系三矩式	∑m_A（F）=0，∑m_B（F）=0，∑m_C（F）=0	3

静定与超静定（静不定）

静定问题：未知力的数目<=静力平衡方程的数目

超静定问题：未知力的数目>静力平衡方程数目

超静定次数：多余约束的数目

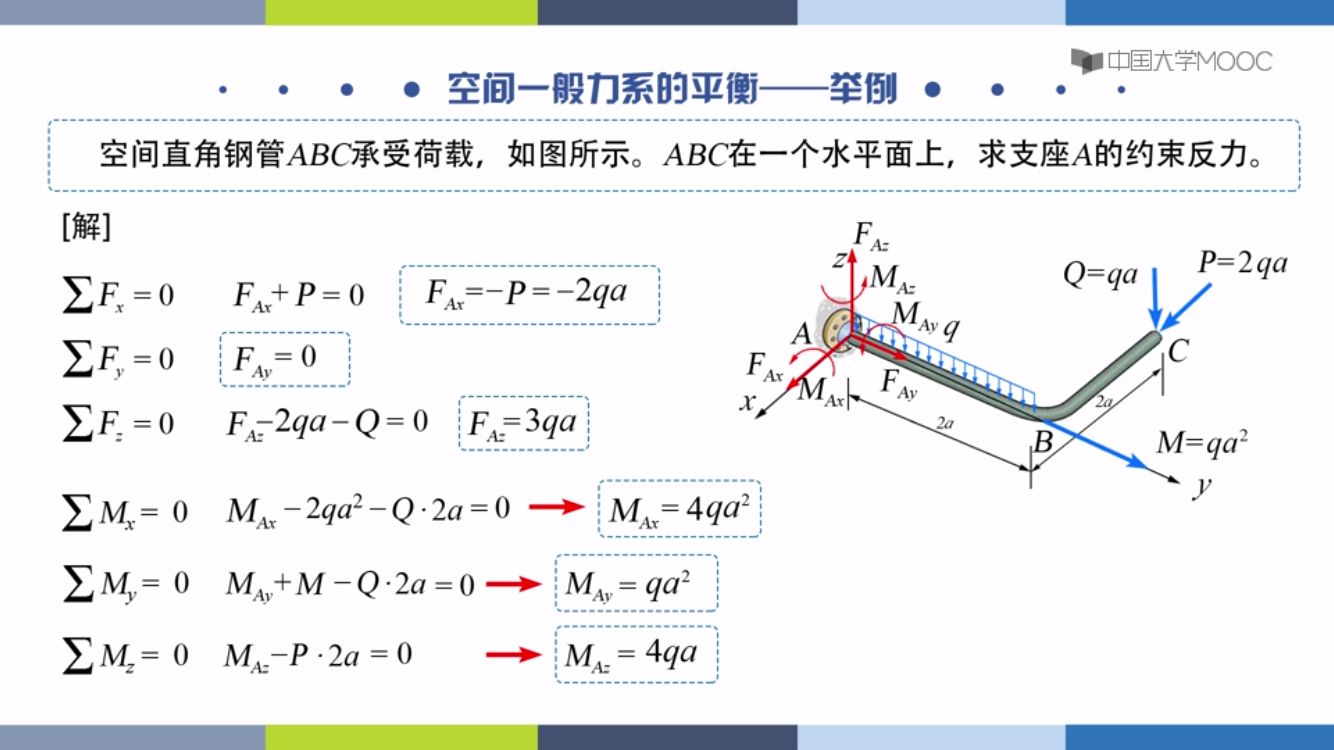
空间力系

有6个约束

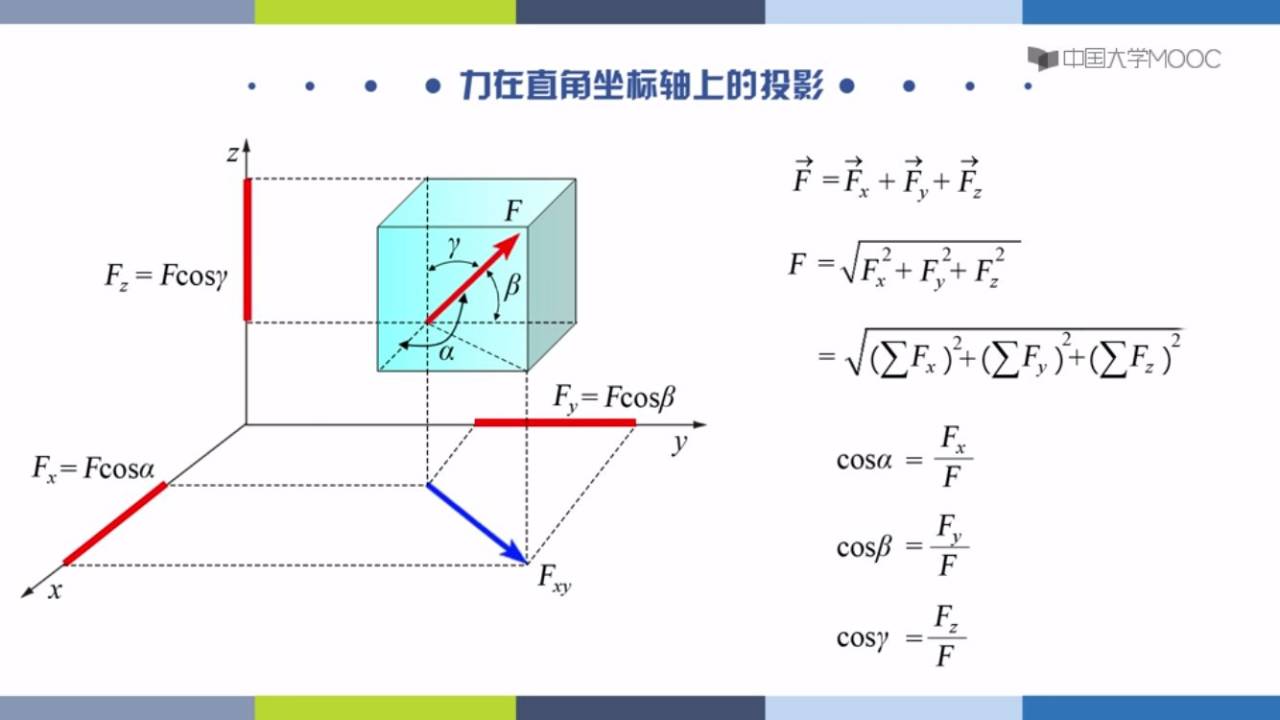
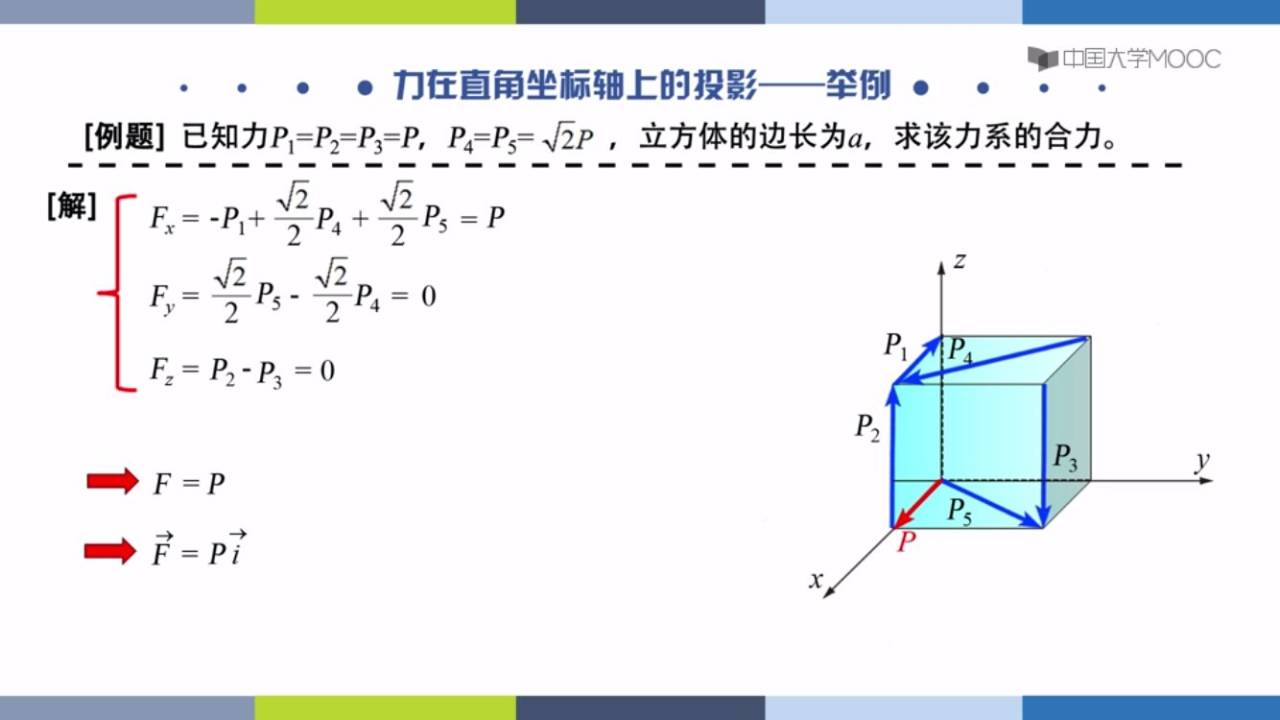
空间汇交力系

有三个平衡方程

$\Sigma F_x=0 \\ \Sigma F_y=0 \\ \Sigma F_z=0$

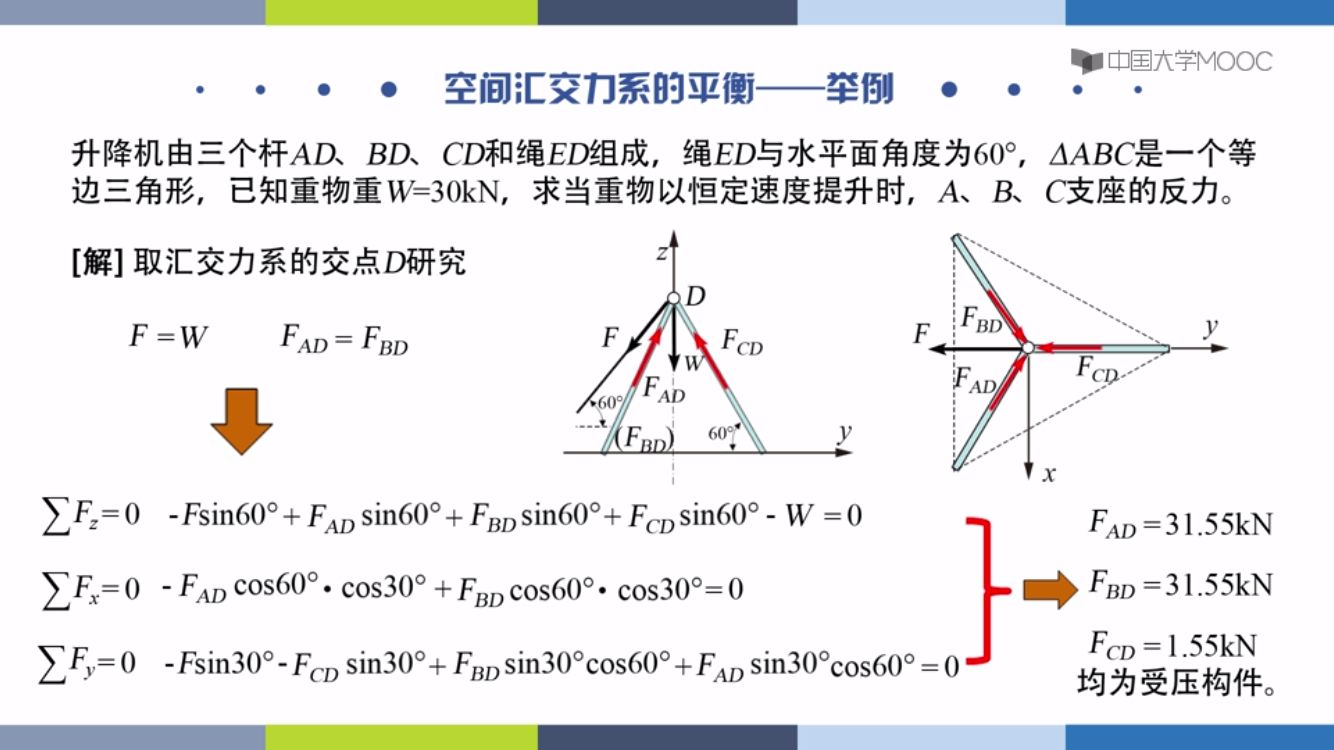
空间力对点之矩

$\overrightarrow r=\overrightarrow x+\overrightarrow y+\overrightarrow z \\ \overrightarrow F=\overrightarrow F_x+\overrightarrow F_y+\overrightarrow F_z$

空间力对轴之矩

$M_z(F)=\pm F_{xy}h$

空间力偶

空间力偶是一个矢量，平面力偶是代数量

$M=Frsin\theta$

$R^‘=0 ,M_0\ne0，和中心位置无关 \\R^‘\ne0 ,M_0=0，和中心位置有关 \\R^‘\ne0,M_0\ne0,和中心有关$

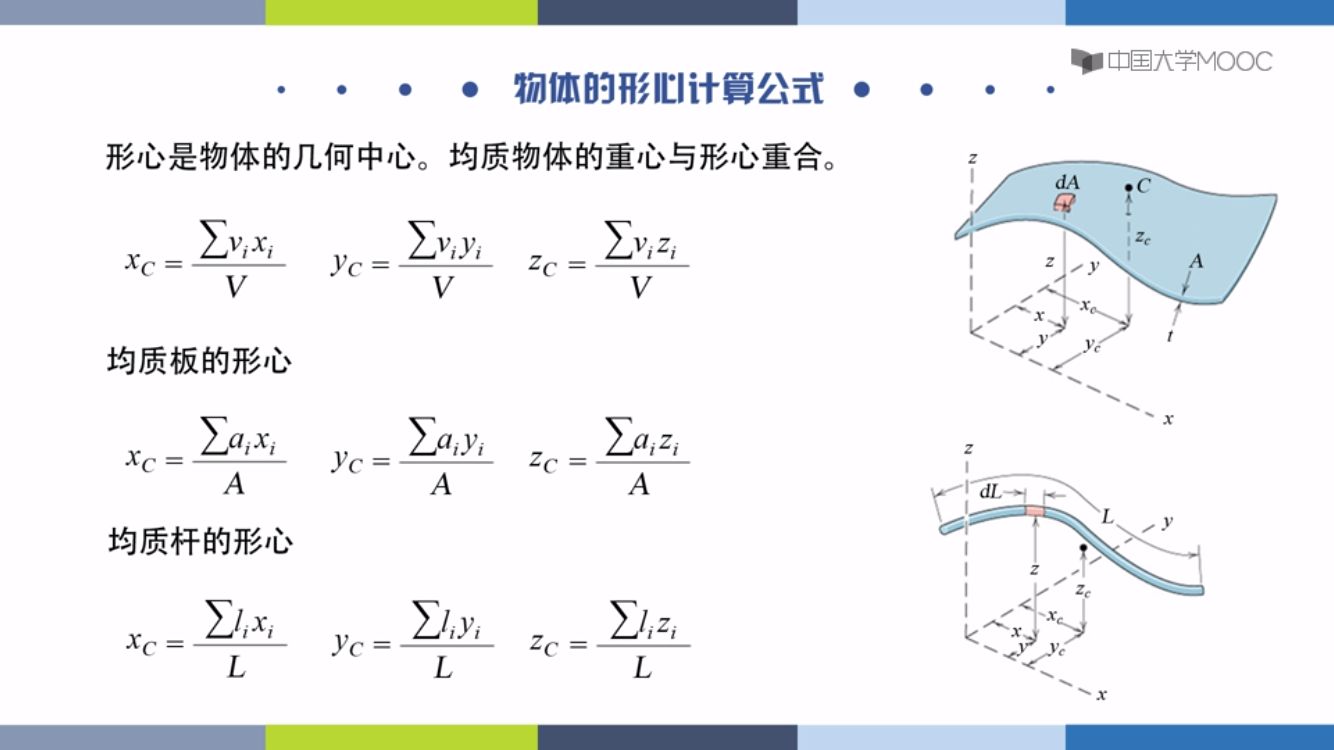
物体重心和形心

重心形心
$C(x_c,y_c,z_c) \\ x_c=\frac{\int x\times dw}{W} \ \ \ \ \ y_c=\frac{\int y\times dw}{W} \ \ \ \ \ \ z_c=\frac{\int z\times dw}{W}$
形心公式

桁架

一种由若干件彼此在两端用铰链连接而成，受力后几何形状不变的结构

节点法计算内力

整体平衡求解支座反力

节点法计算杆件内力

截面法计算内力