材料力学
内力
外部力引起的内部相互作用
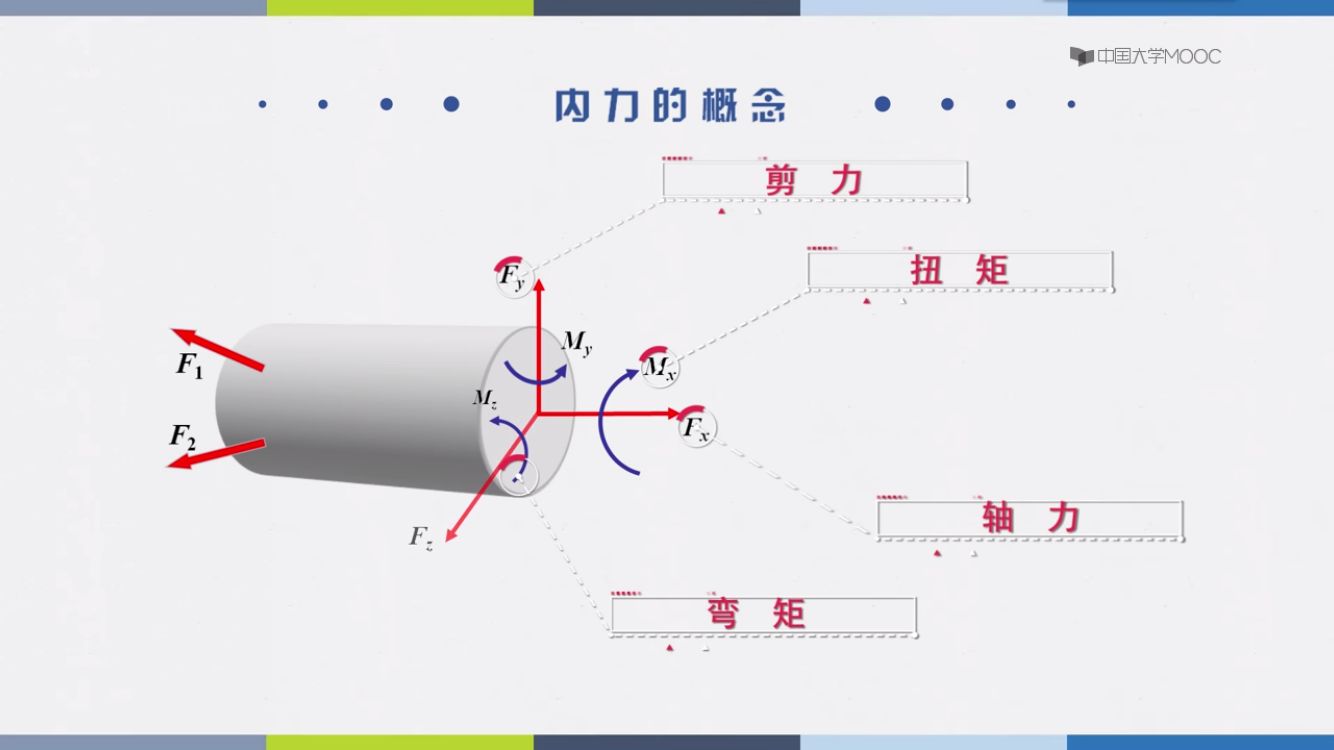
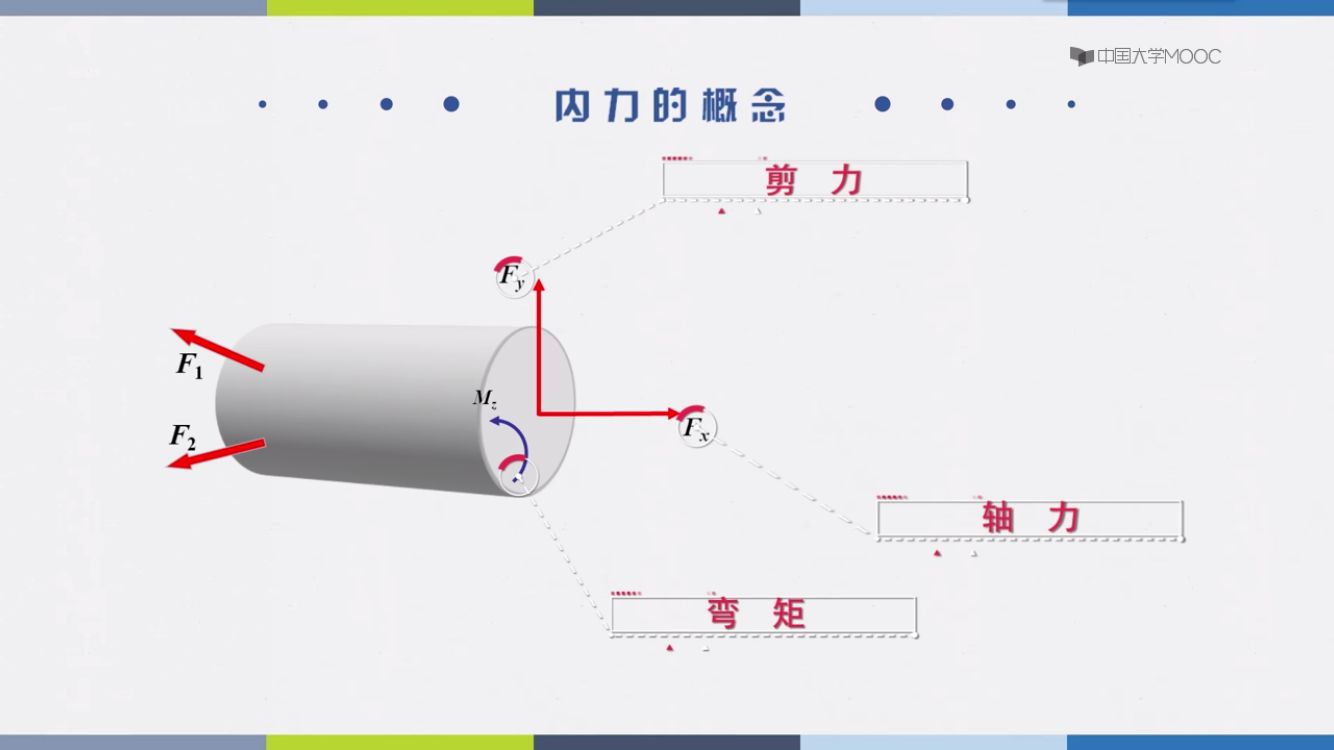
对用平面研究只有这个三个力。
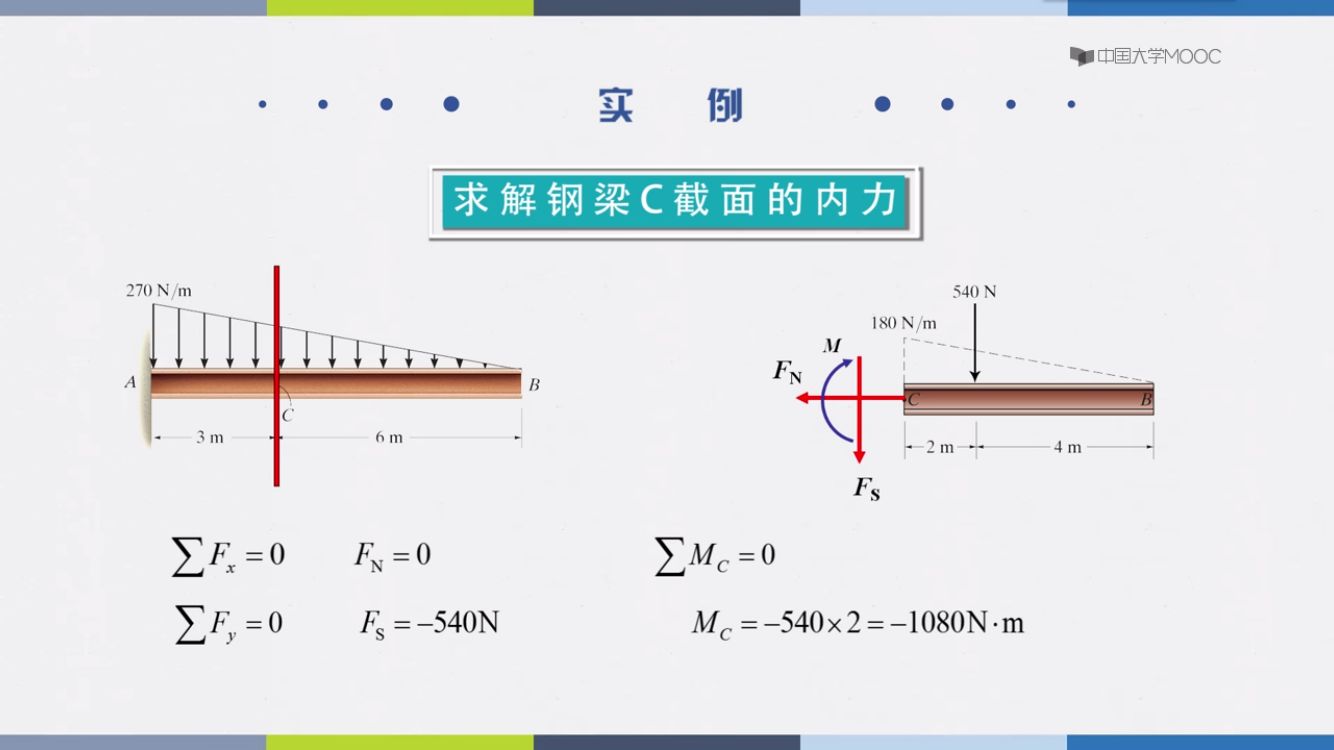
研究C点的内力,需要将物从C点分开,根据关系可知C点的力为180N/m,总压力是三角形的面积520N(在距离C三分之一杆长处,我也知道为啥)
因为平衡 ΣFx=0 FN=0 同理 ΣFy=0 FS=−540N 同理 ΣMC=0 力乘扭矩 Mc=−540×2=−1080N
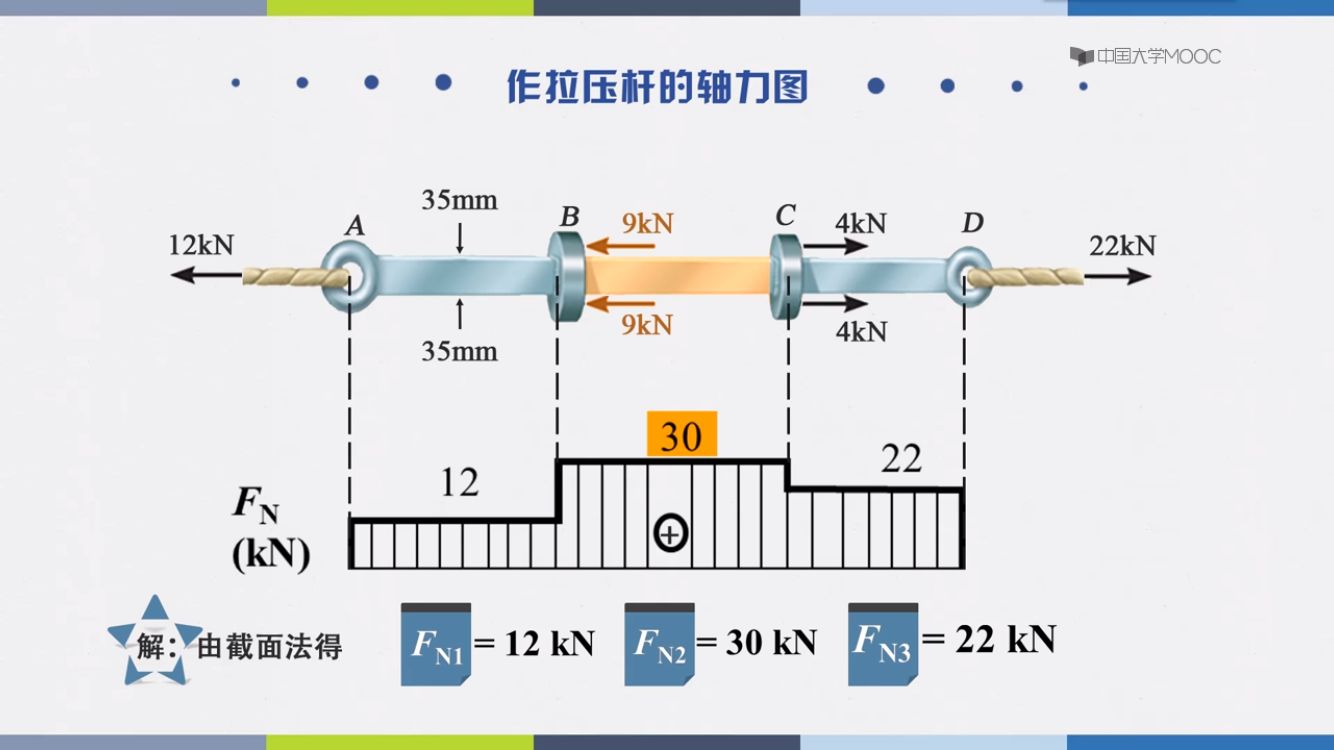
轴力图
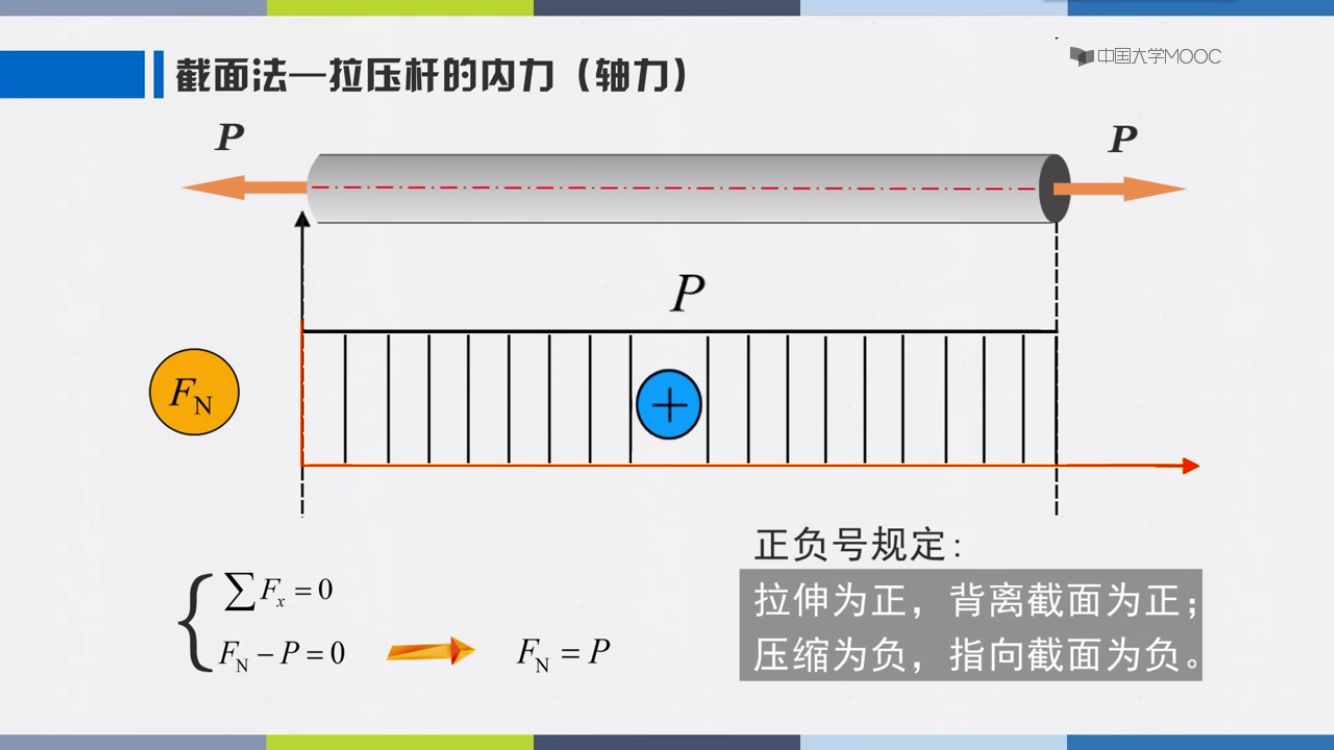
拉正,压负
三个截面,分别研究
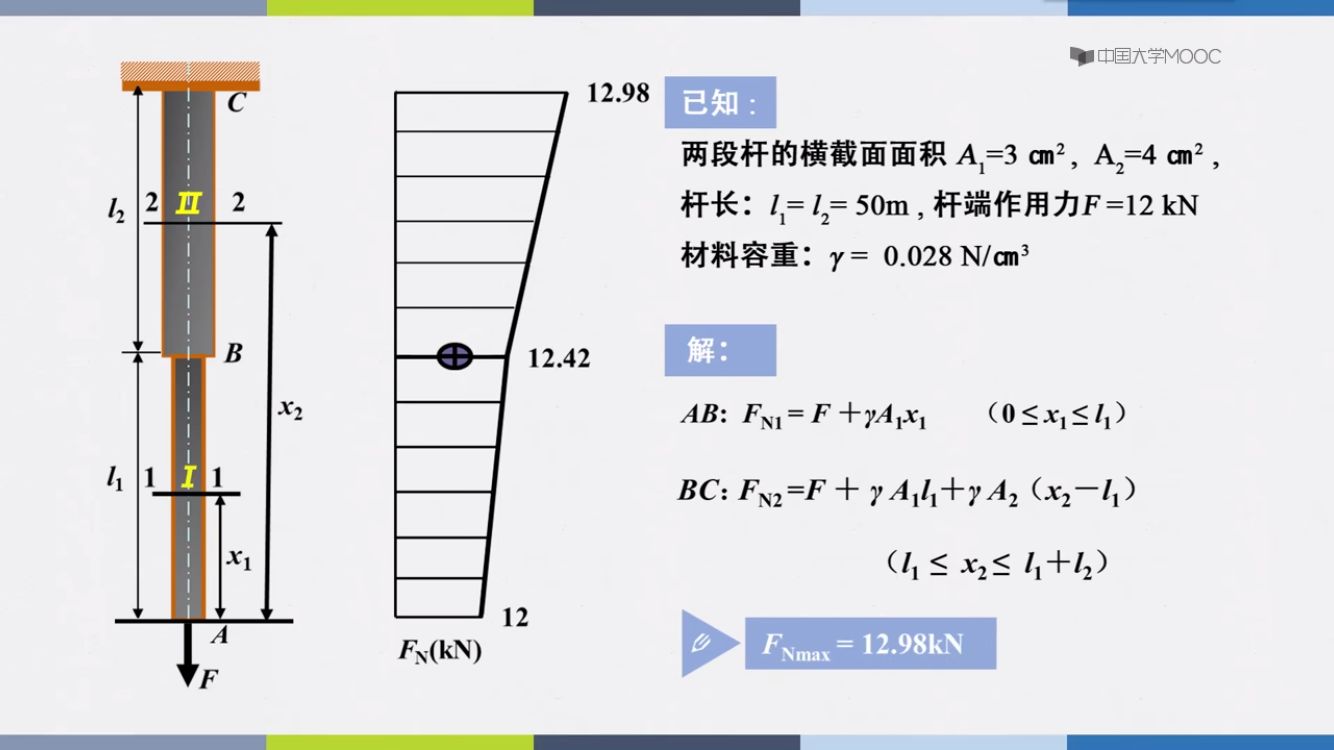
容重:单位体积的重量
截面法求内力
截开,代替,平衡
应力
概念:
内力在一点处的分布集度,表达材料强度的物理量。(应力不是力,是单位面积上的内力)
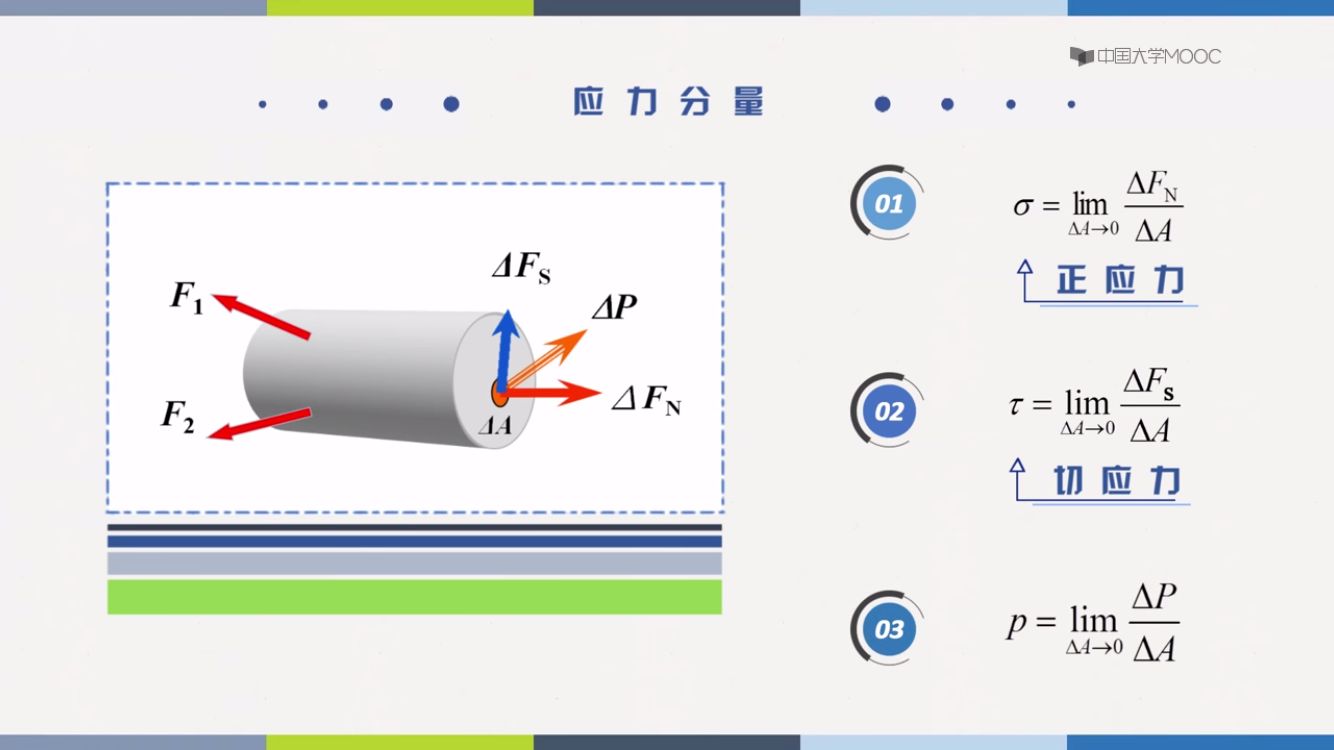
正应力:垂直于切面的力,轴力(N)/面积(A)
切应力:平行于切面的力
应力集中系数:k=最大的应力/平均应力
单位:
1Pa=1N/m2
1MPa=106Pa
1GPa=109Pa
弯曲正应力
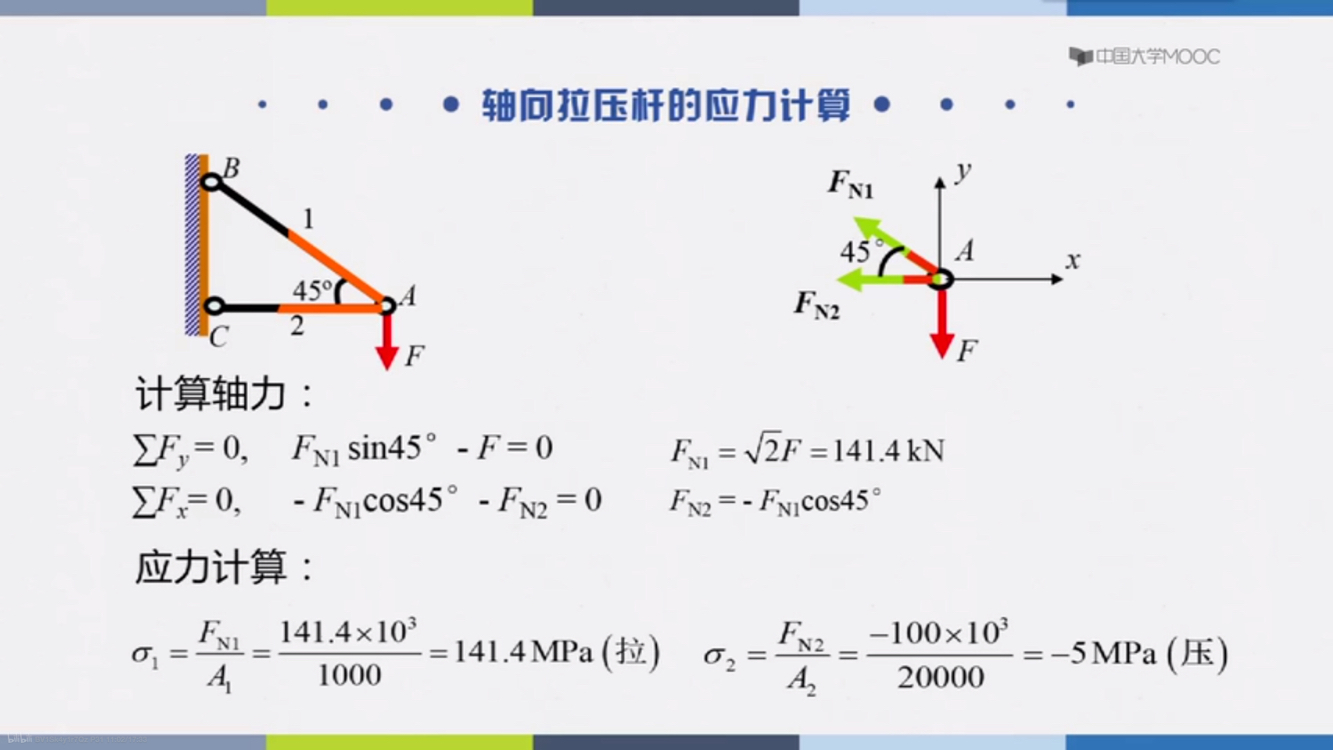
轴向拉压应力计算

极限应力(σu):材料发生破坏时,能够承担的最大应力
安全因数(n):极限应力与许用应力之比大于1的系数
许用应力([σ]):构件工作时被允许承受的最大工作应力
[σ]=nσu
校核强度
σmax=(AFN)≤[σ]
极限载荷
FNmax≤A[σ]
拉压杆变形

纵向线应变:ε=LΔL横向线应变:ε′=bΔb泊松比:υ=∣εε′∣拉压杆变形计算公式:Δl=EAFNl阶梯杆总变形:Δl=i=1∑nEiAiFNili积分求解:Δl=∫lEA(x)FN(x)dx
拉压应变能(Vε)
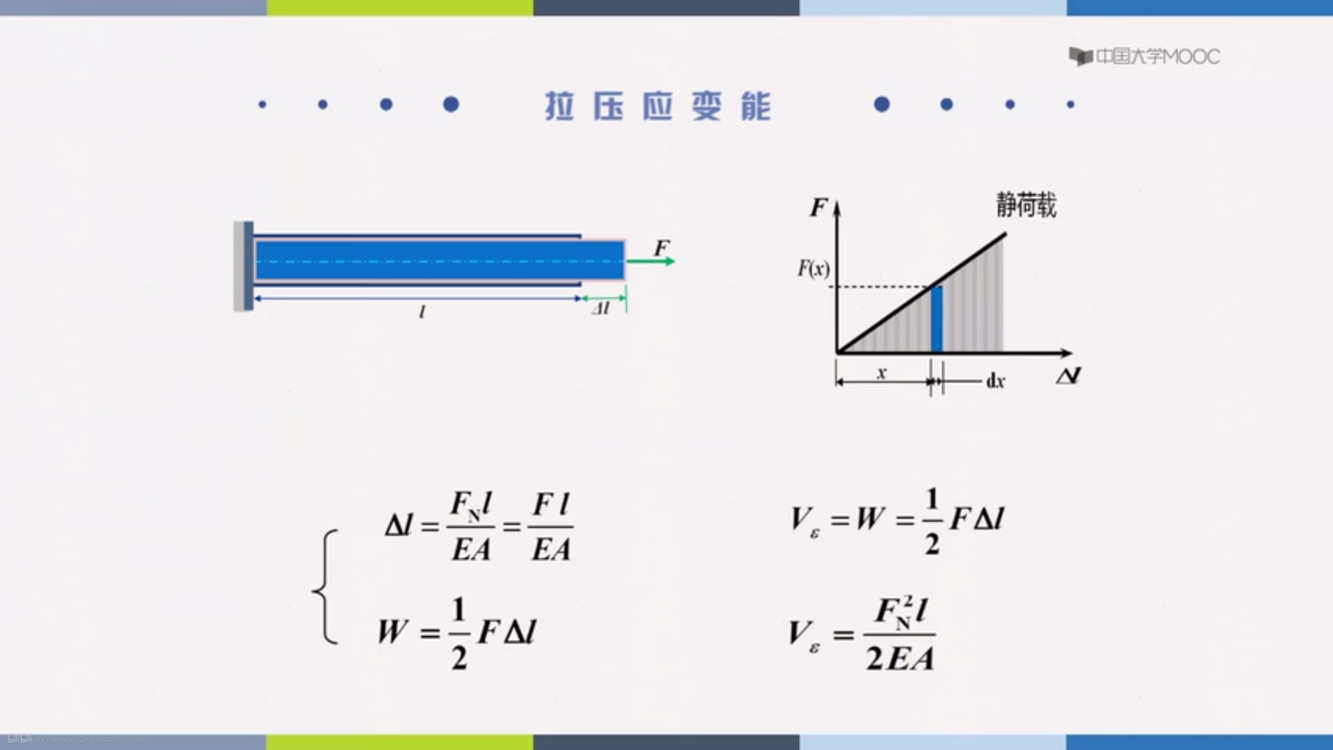
{Δl=EAFNl=EAFlW=21FΔlVε=W=21FΔlVε=2EAFE2l
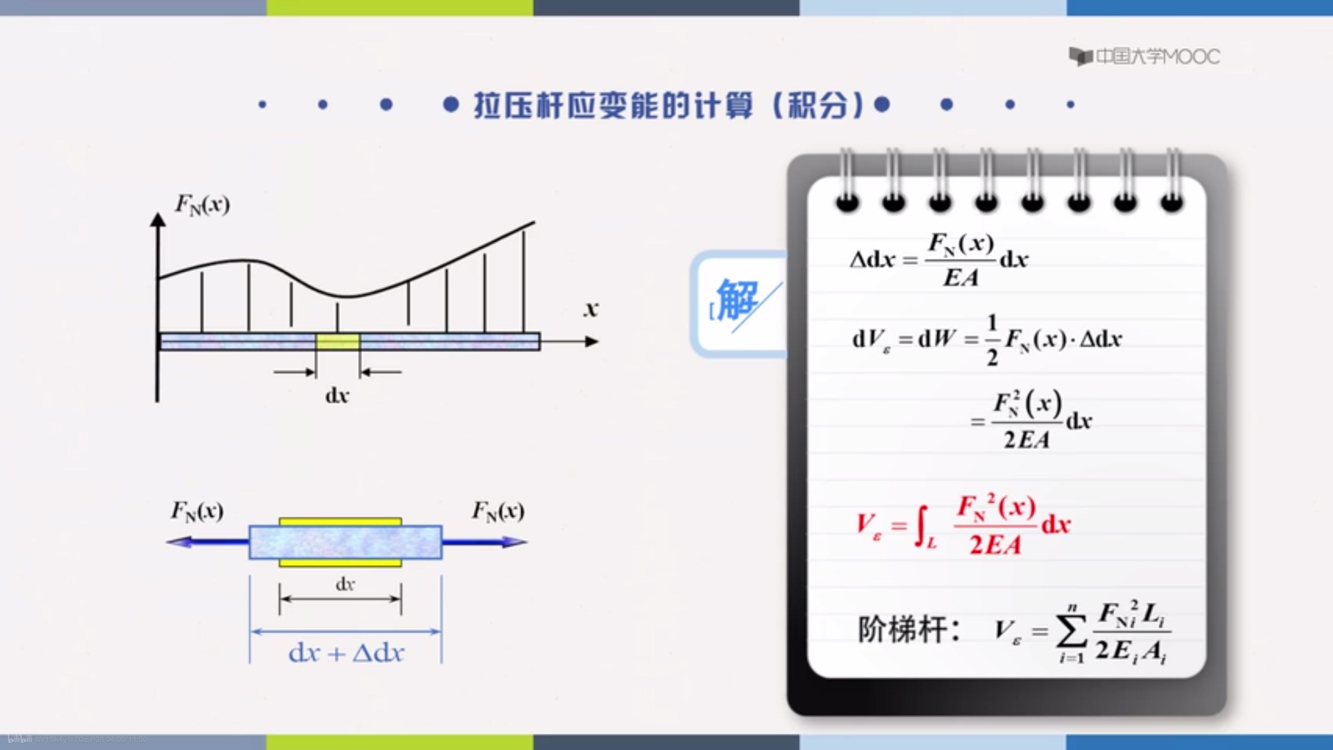
应变能密度(νε)

νε=21σε=2Eσ2=2Eε2
低碳钢拉伸
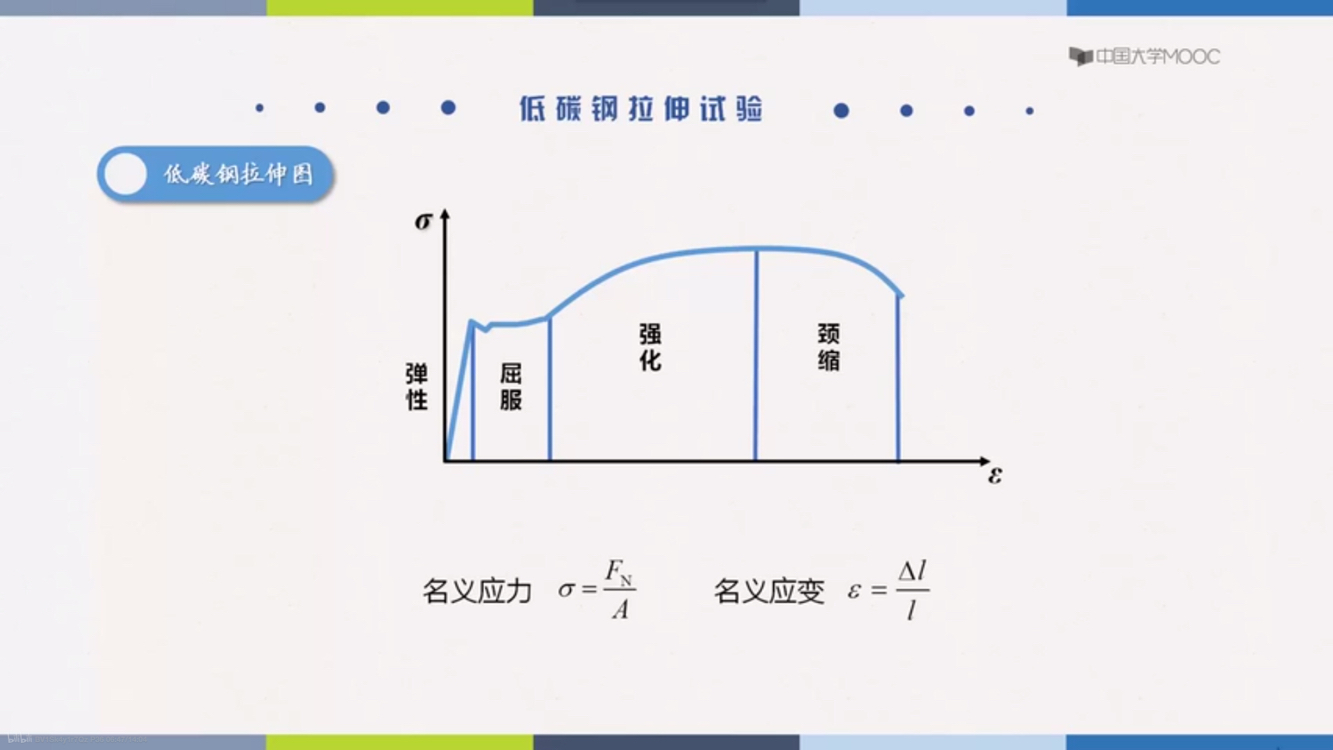
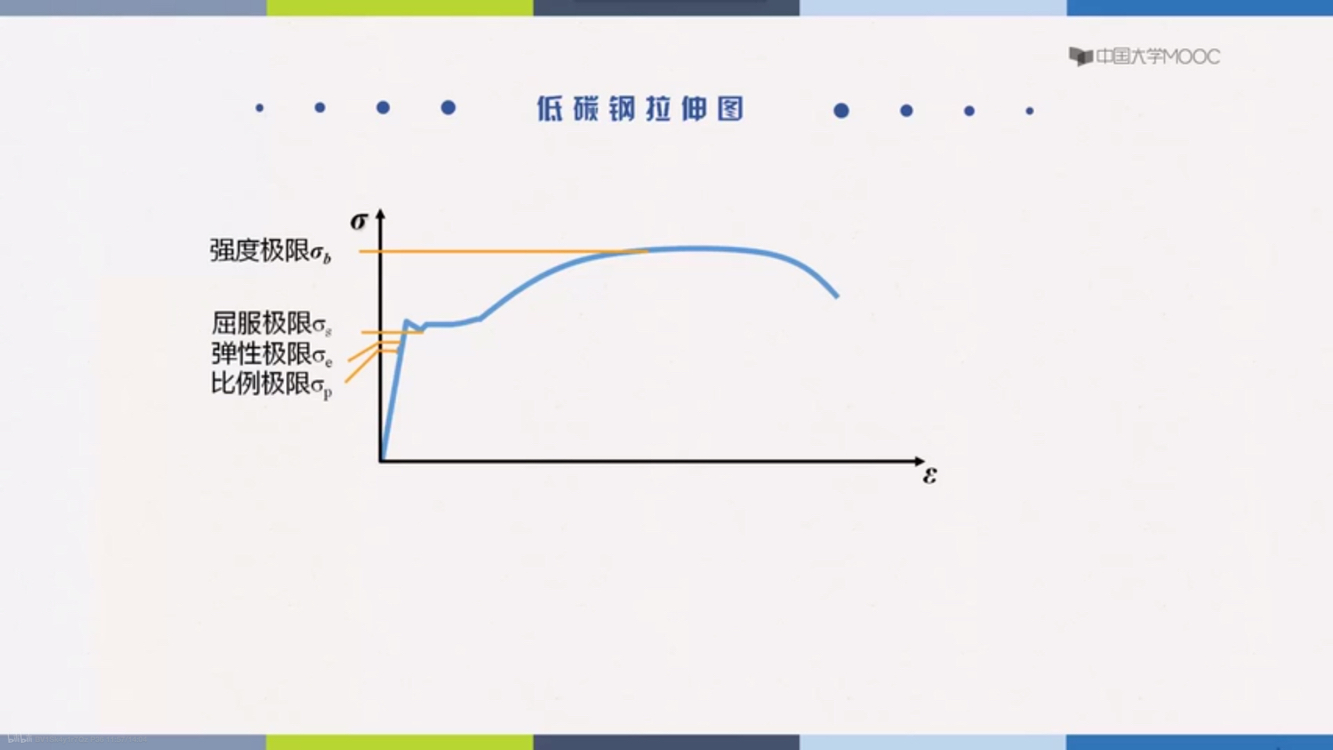
比例极限:σp弹性极限:σe屈服极限:σs强度极限:σb
塑性材料指标

断面收缩率

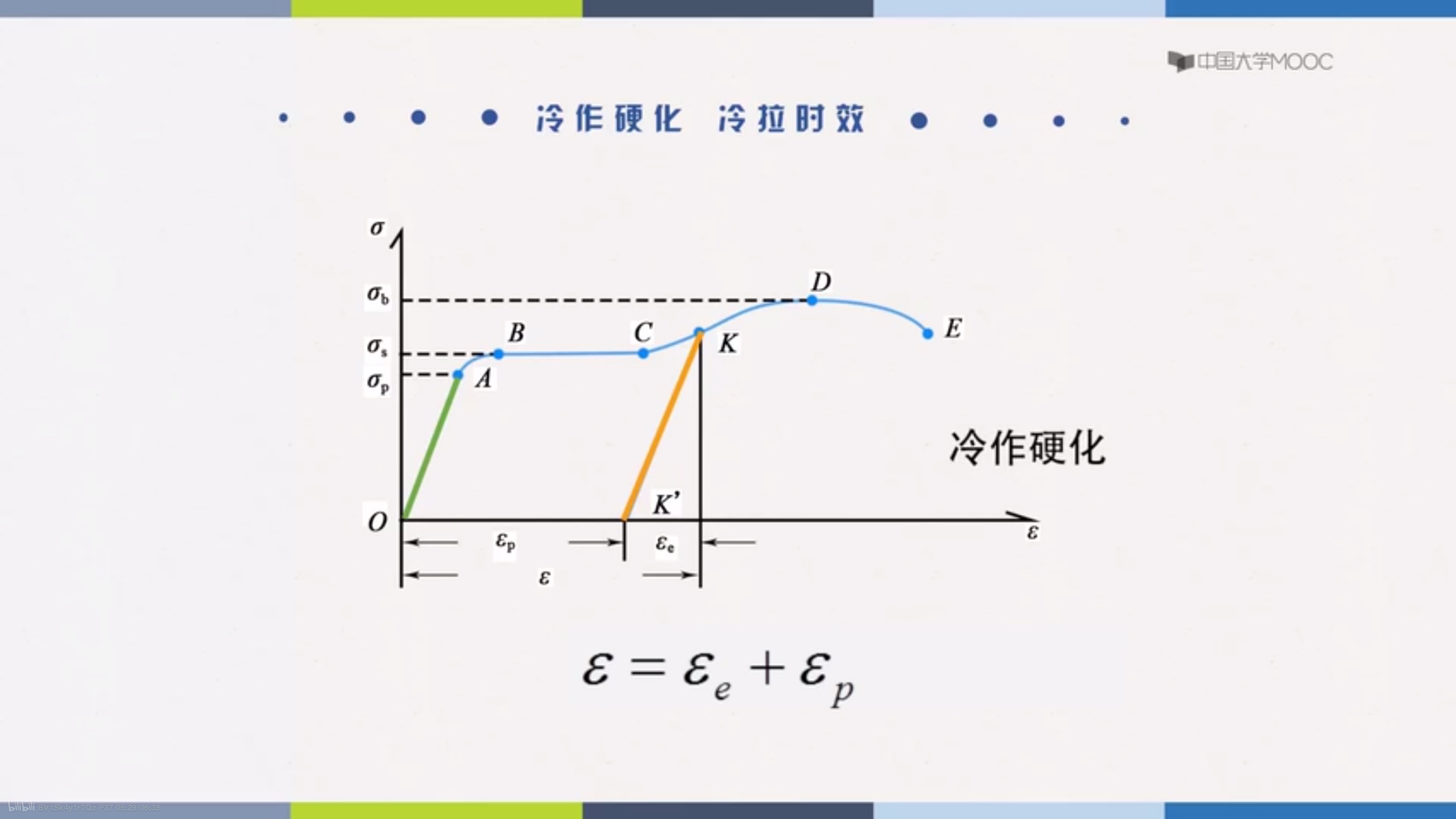
冷作硬化
加载卸载再加载,提高弹性极限,形变能力下降,隔段时间再次进行,这种叫做(冷拉时效)
应力集中
只和几何形状有关系
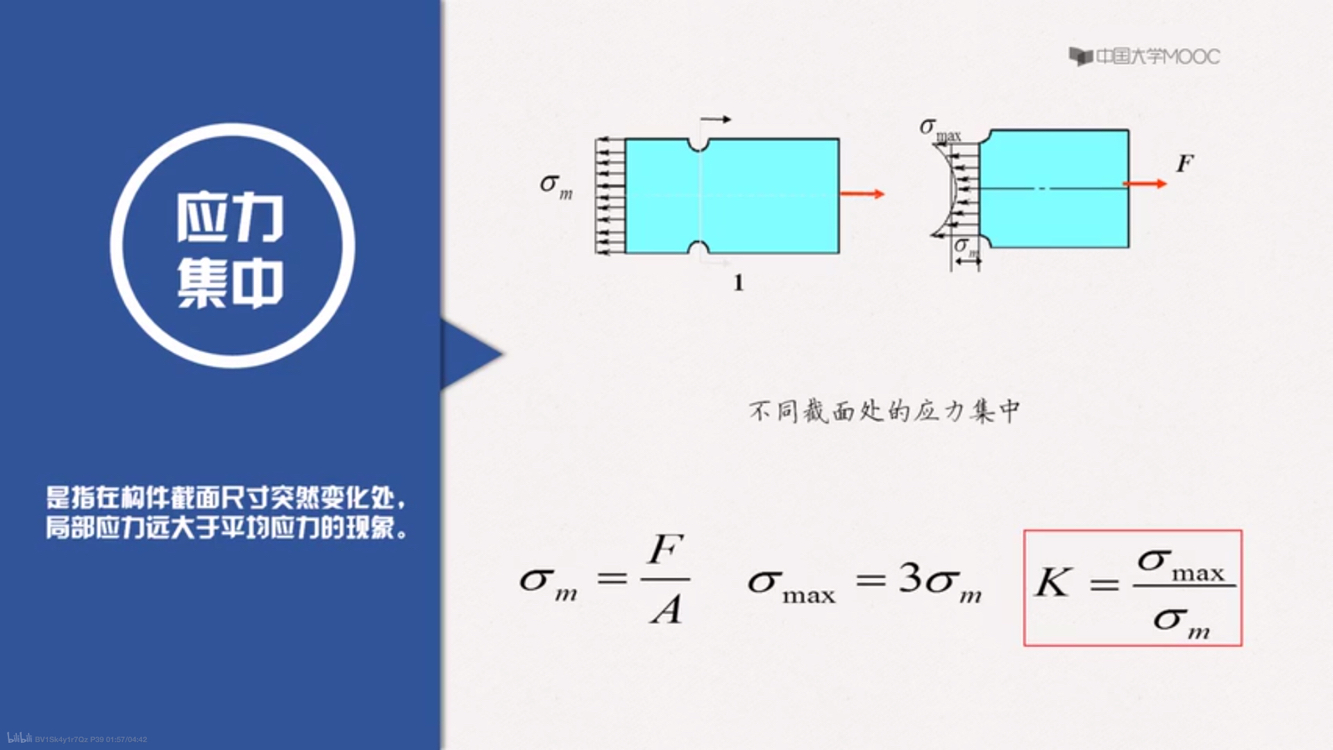
σm=AF σmax=3σm K=σmσmax
失效应力
脆性材料无屈服,无塑性可变
延伸率
δ=LL1−L×100%脆性材料<5%,塑性材料>5%
截面收缩率
ψ=AA−A1×100%
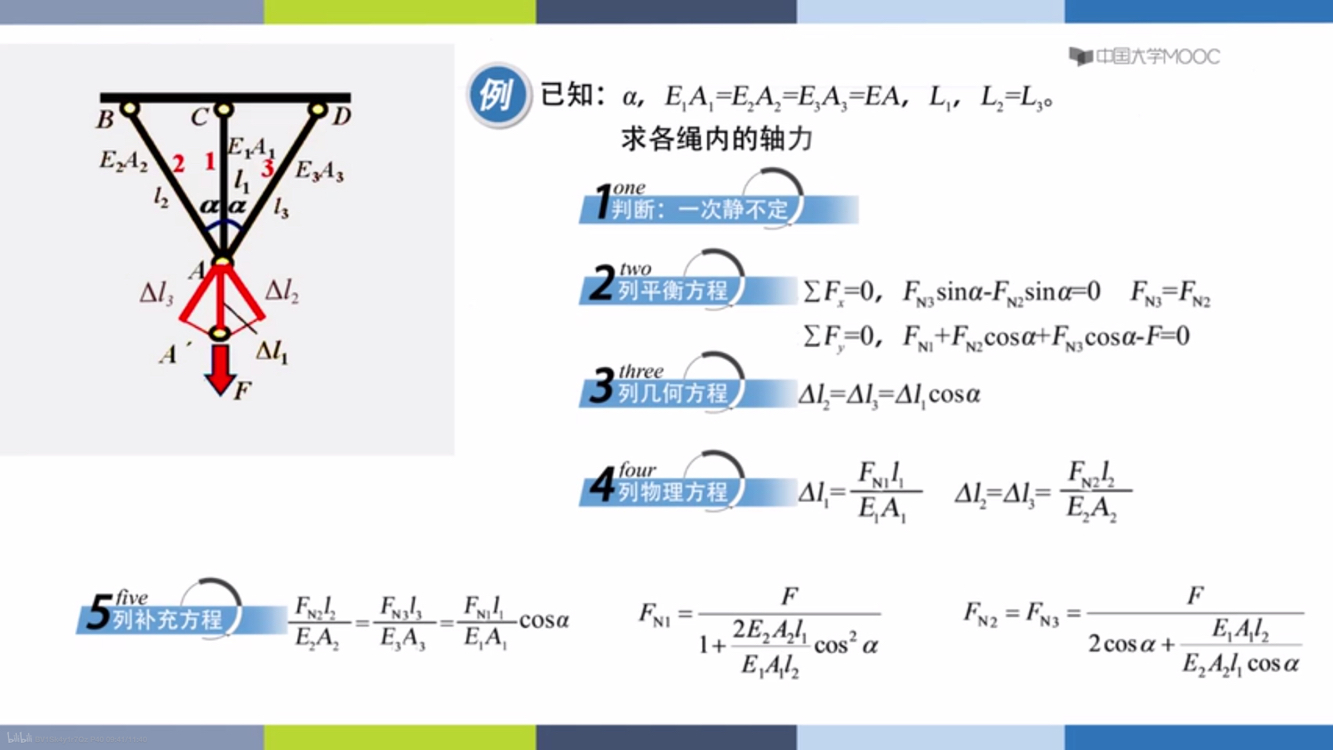
解超静定问题
列出补充方程
应变
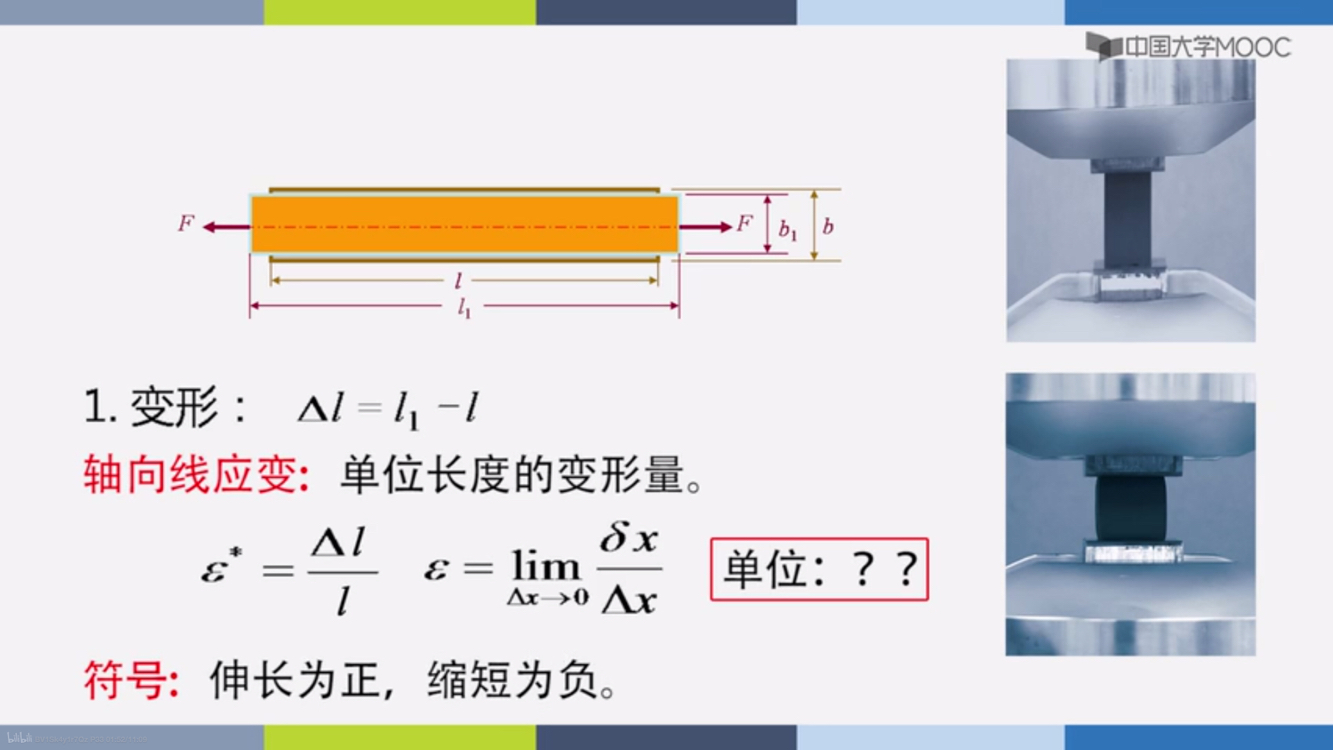
绝对变形:
Δl=l1−ll1是力作用后的
线应变
ε=lΔl
胡克定律(应变应力关系)
E−弹性模量σ=Eεσ=AN ε=lΔl轴向形变 EA−抗拉刚度Δl=EANl
应变能
积存在弹性体内的应变能等于外力所作的功:Eε=W
W=21FΔL
应变能密度
e=VEε=21σε
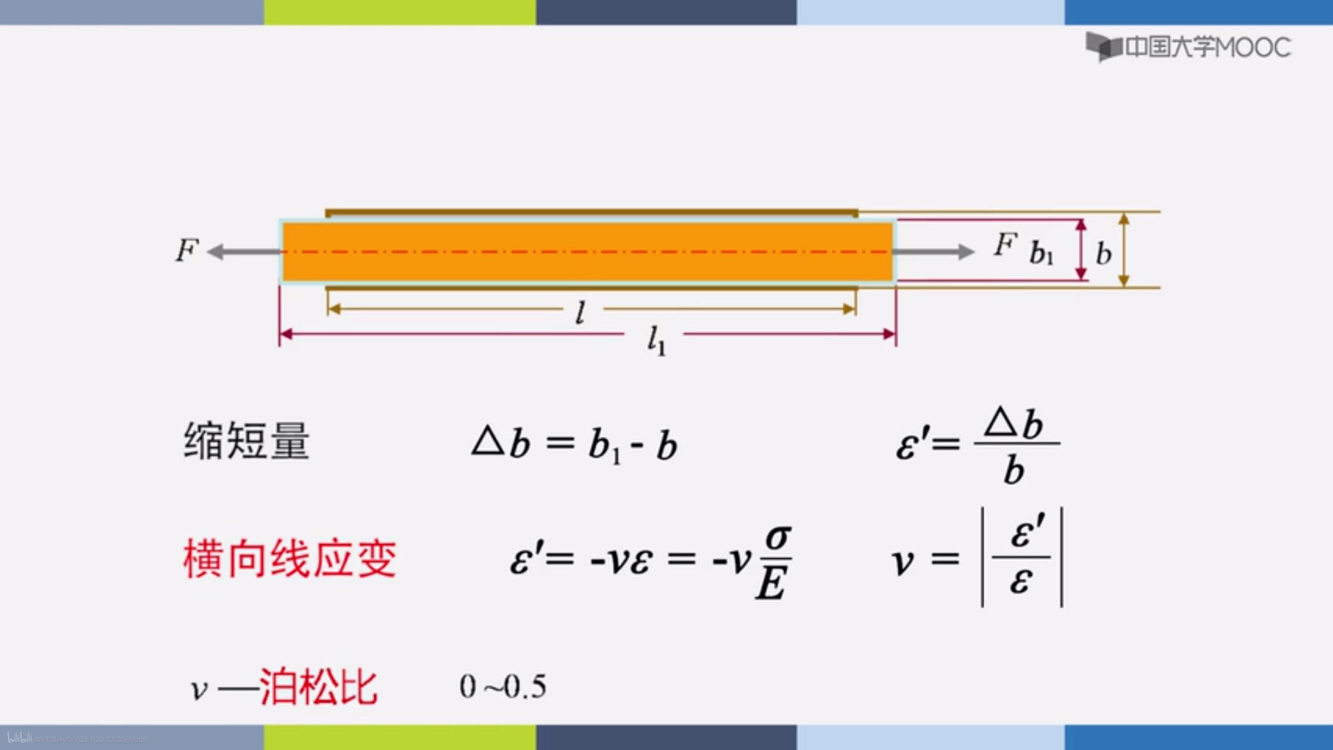
杆横向的变形
横向形变
Δb=b1−bb1是力作用后的
横向应变
ε′=bΔb
泊松比0~0.5之间
负的横向应变除以纵向应变
μ=−εε′
剪切























