函数的概念与特性
函数
函数的概念与特性:按照对应
法则x在给定的所有集里都有唯一的y与之对应,称为y为x的函数,x是自变量y是因变量,集是定义域
y=f(x) y因变量,f()对应法则,x自变量
分子有理化
指的是在二次根式中分母原为无理数,而将该分母化为有理数的过程,也就是将分母中的根号化去。
单项式:a1=aaa=aa二项式:a+b1=(a+b)(a−b)(a−b)=a−b2a−b
一般运算
⎩⎪⎨⎪⎧y=ln(x+1)ey=eln(x+1)ey=x+1 uv=elnuv=evlnu,u和v都是函数=====================================arcsinx+arccosx=2π(−1≤x≤1)证:(arcsinx+arccosx)′=1−x21−1−x21=0arcsinx+arccosx=Cx=0时C=2π=====================================arcsinx+arccosx=2π(−∞<x<∞)证:同理
对数运算法则
loga(MN)=logaM+logaNloga(NM)=logaM−logaNlogaMn=nlogaMlnx1=−lnxlnx=lnx21=21lnxln(1+x1)=lnxx+1=ln(x+1)−lnx
一元二次方程
ax2+bx+c=0求根x1,2=2a−b±b2−4ac韦达定理x1+x2=−ab,x1x2=ac判别式Δ=b2−4ac,Δ>0俩不等实根Δ=0俩等实根Δ<0无实根俩共轭复根顶点(−2ab,c−4ab2)
因式分解公式
(a+b)2=a2+2ab+b2 , (a−b)2=a2−2ab+b2(a+b)3=a3+3a2b+3ab2+b3 , (a−b)3=a3−3a2b+3ab2−b3(a+b)n=k=0∑nCnkan−kbk,C可以使用杨辉三角⎩⎪⎪⎪⎨⎪⎪⎪⎧C00=1C10,C11=1,1C20,C21C22=1,2,1...a2−b2=(a+b)(a−b)a3+b3=(a+b)(a2−ab+b2) , a3−b3=(a−b)(a2+ab+b2)an−bn=(a−b)(an−1+an−2b+...+abn−2+bn−1)an+bn=(a−b)(an−1−an−2b+...−abn−2+bn−1)
阶乘与双阶乘
0!=1n!=1⋅2⋅3⋅...⋅n(2n)!!=2⋅4⋅6⋅...⋅(2n)=2n⋅n!(2n−1)!!=1⋅3⋅5⋅...⋅(2n−1)华里士公式用到双阶乘
不等式
∣a±b∣≤∣a∣+∣b∣,∣∣a∣−∣b∣∣≤∣a−b∣,拓展{∣a1±a2±...±an∣≤∣a1∣+∣a2∣+...+∣an∣∣∫abf(x)dx∣≤∫ab∣f(x)∣dxab≤2a+b≤2a2+b2,(a,b>0)3abc≤3a+b+c≤3a2+b2+c2,(a,b,c>0)a>b>0则{n>0,an>bnn<0,an<bn0<a<x<b,0<c<y<d,bc<xy<adsinx<x<tanx(0<x<2π)sinx<x(x>0)arctanx≤x≤arcsinx(0≤x≤1)ex≥x+1x−1≥lnx(x>0)1+x1<ln(1+x1)<x1(x>0)
反函数
概念:y=f(x)如果y对应的每一个定义域,都有x对应的值域则x=φ(y)为反函数严格单调函数必有反函数,有反函数不一定严格单调
函数和反函数关于y=x对称是字母互换的结果
y=2x => x=21y 这两个函数图像是一个字母互换y=21x和y=2x关于y=x对称
复合函数
y=f(u),u=g(x)=>y=f[g(x)](x∈D)叫复合函数
第一题
设f(x)=x2,f[φ(x)]=−x2+2x+3,且φ(x)≥0,求φ(x)及其定义域与值域解:f[φ(x)]=φ2(x)=−x2+2x+3φ2(x)=−x2+2x+3φ(x)=−x2+2x+3根号下不为零:−x2+2x+3≥0=>x∈[−1,3]φ(x)=−(x−1)2+4(x−1)2越小φ(x)越大,反之亦然x=1,φ(x)=2x=−1或3,φ(x)=0φ(x)∈[0,2]
第二题
求函数y=f(x)=ln(x+x2+1)的反函数f−1(x)的表达式及其定义域解:y=ln(x+x2+1)ey=x+x2+1 ,fun1−y=−ln(x+x2+1)=ln(x2+1+x1)=ln(1x2+1−x)e−y=x2+1−x ,fun2fun1−fun2=2ey−e−y=x所以:x=f−1(y)=2ey−e−y则:y=f−1(x)=2ex−e−x
拓展
y=ln(x+x2+1)
这个函数叫反双曲
正弦
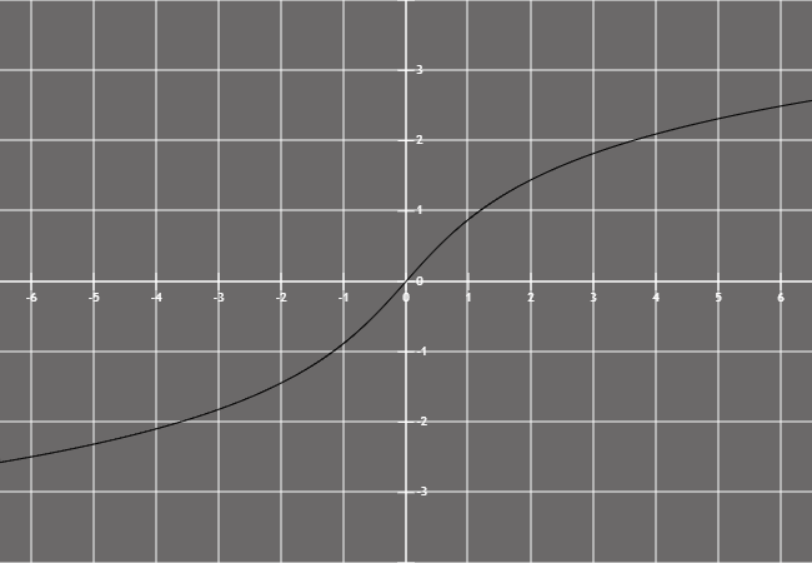
y=2ex−e−x
这个函数叫双曲正弦
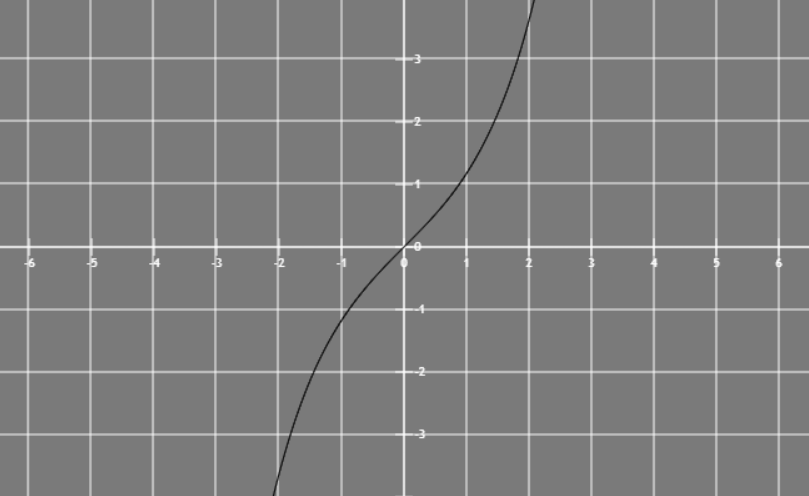
y=2ex+e−x
这个函数叫双曲余弦,悬链线的一种
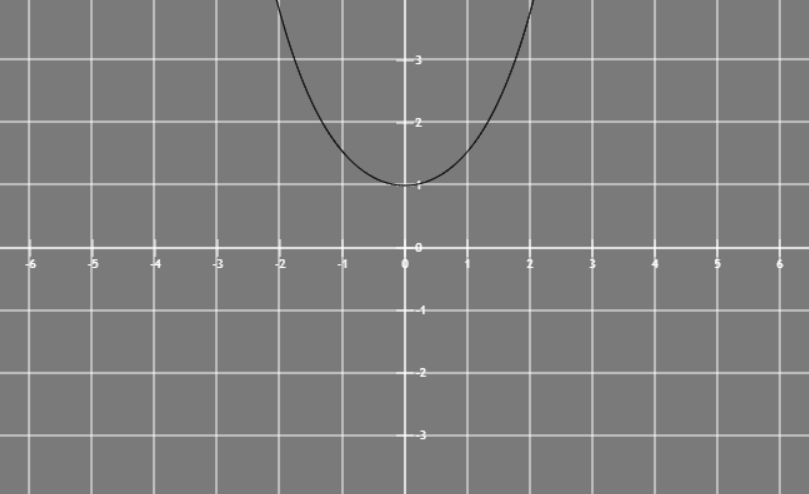
第三题
将下列各组函数f(x)与φ(x)复合,求复合函数f[φ(x)]f(x)={2−x,x≤0x+2,x>0φ(x)={x2,x<0−x,x≥0
解法如下:
1,解 广义化f:[φ(x)]={2−φ(x),φ(x)≤0φ(x)+2,φ(x)>0
画图:
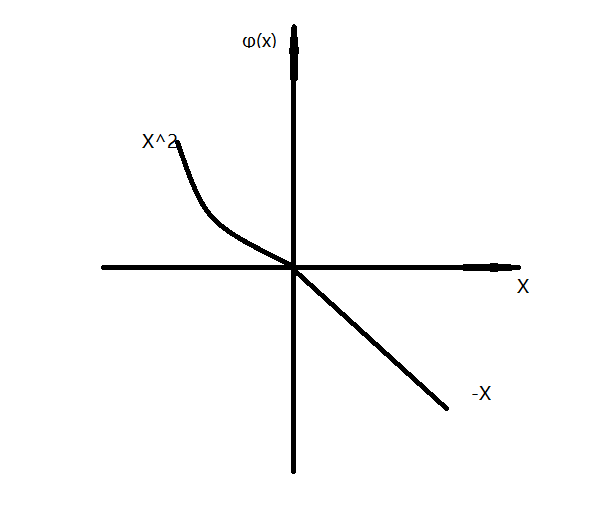
如图当φ(x)≥0时x的范围为大于等于零,推出f[φ(x)]={2−(−x),x≥0x2+2,x<0
特性
有界性
有界无界指明区间
有界是指的纵坐标上有限度
单调性
区间内自变量增减函增(单调增)
区间内自变量减函数减(单调减)
判断方法:
f’(x)>0 单调增
f’(x)<0 单调减
(x1−x2)[f(x1)−f(x2)]>0 单调增(x1−x2)[f(x1)−f(x2)]>0 单调减(x1−x2)[f(x1)−f(x2)]≥0 单调不减(x1−x2)[f(x1)−f(x2)]≤0单调不增
奇偶性
奇函数关于原点对称
f(-x)=-f(x)
F1=f(x)−f(−x) 必为奇函数f(0)=0
偶函数关于y轴对称
f(-x)=f(x)
F1=f(x)+f(−x) 必为偶函数f′(0)=0
关于x=T对称则:f(x)=f(2T-x)或f(T+x)=f(T-x)
周期性
重要结论
若f(x)是可导偶函数,则f’(x)是奇函数
若f(x)是可导奇函数,则f’(x)是偶函数
若f(x)是可导的周期为T,则f’(x)也是周期为T
连续的奇函数的一切原函数都是偶函数
连续的偶函数的原函数中仅有一个原函数是奇函数
若f(x)在有限区间(a,b)内可导且f’(x)有界,则f(x)在(a,b)内有界
若连续函数f(x)以T为周期且∫0Tf(x)dx=0,则f(x)的一切原函数也以T为周期
函数图像
函数图像
lnx
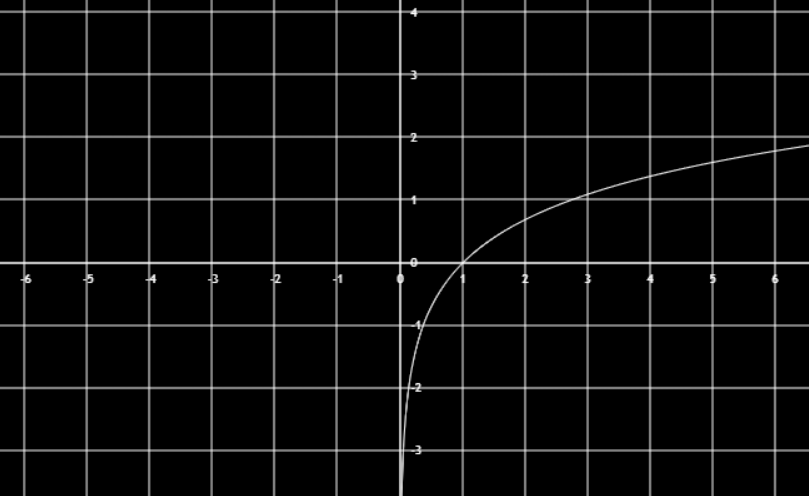
kf(x)伸缩变换,k>1,纵坐标变大,0<k<1,纵坐标变小,横坐标都不变
幂函数
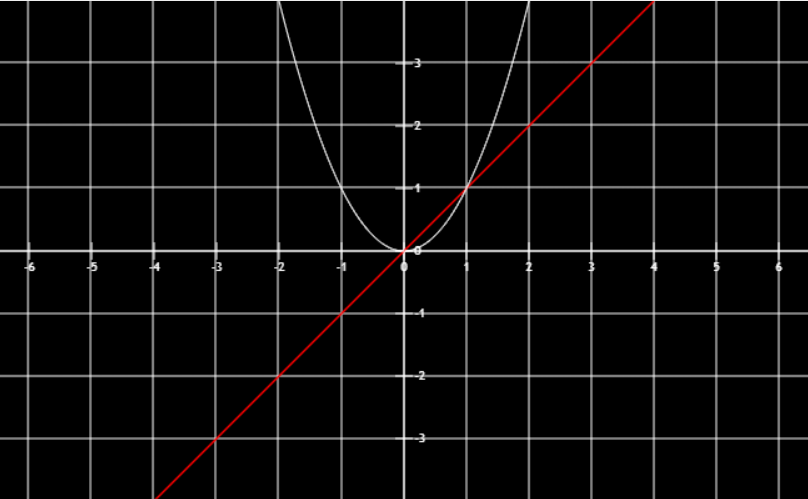
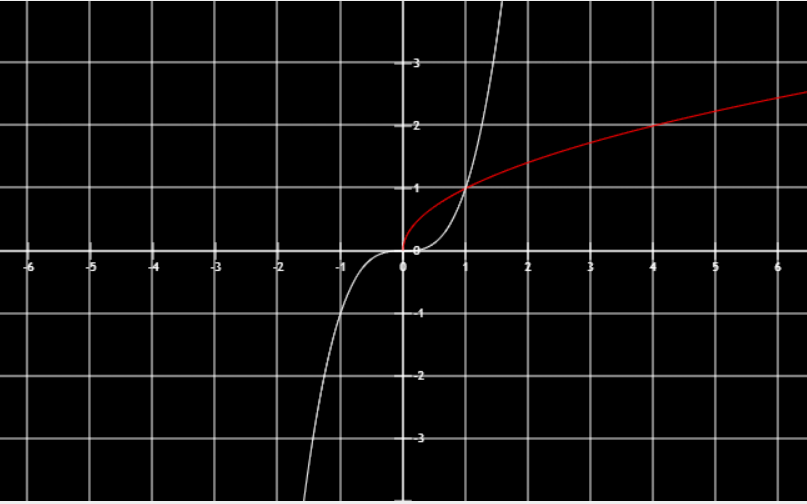
研究x或3x等最值只需要研究x即可研究∣u∣=x2最值只要研究x2
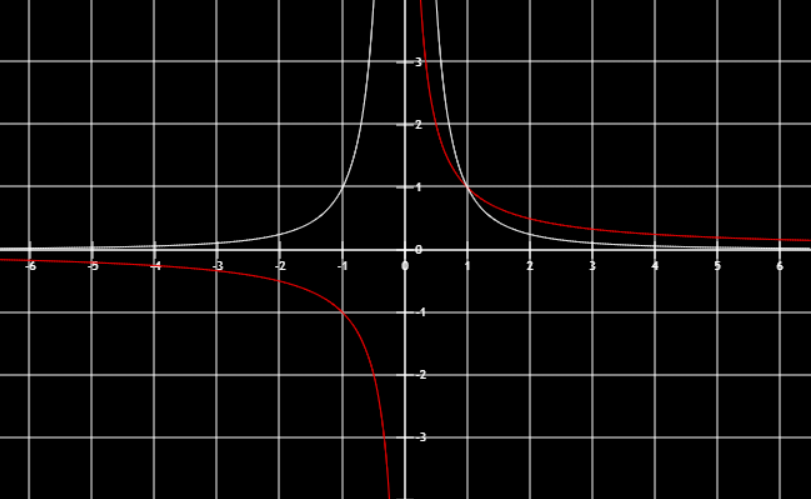
研究x1最值只要研究x,x最大x1最小u1u2...un=u研究i=1∑nui=lnu
指数函数
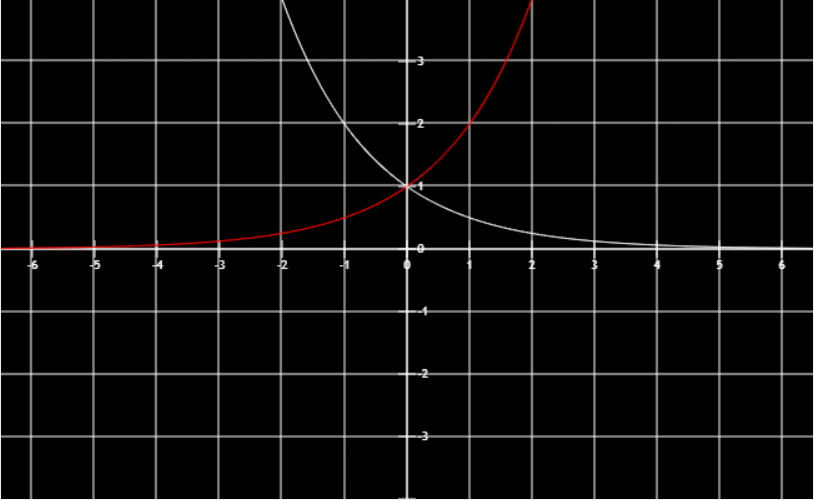
幂指函数
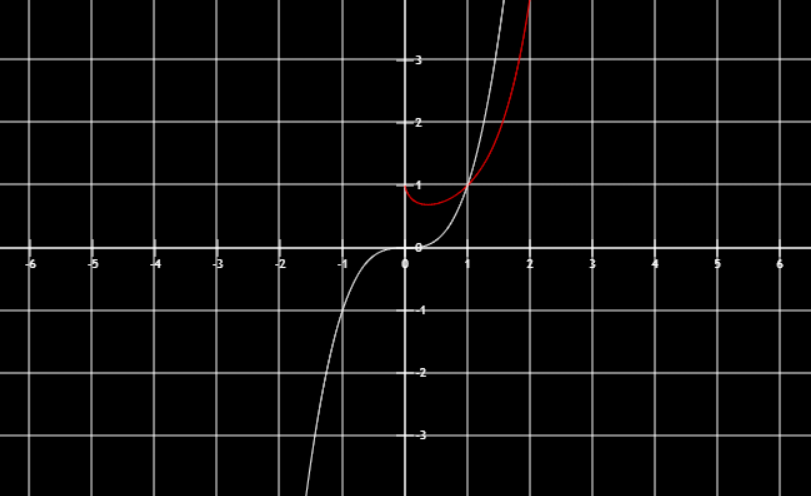
xx极小值点e1
三角函数
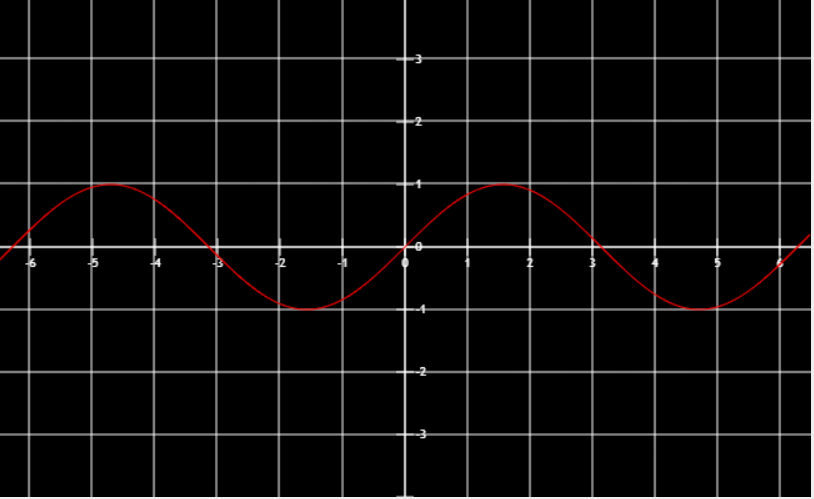
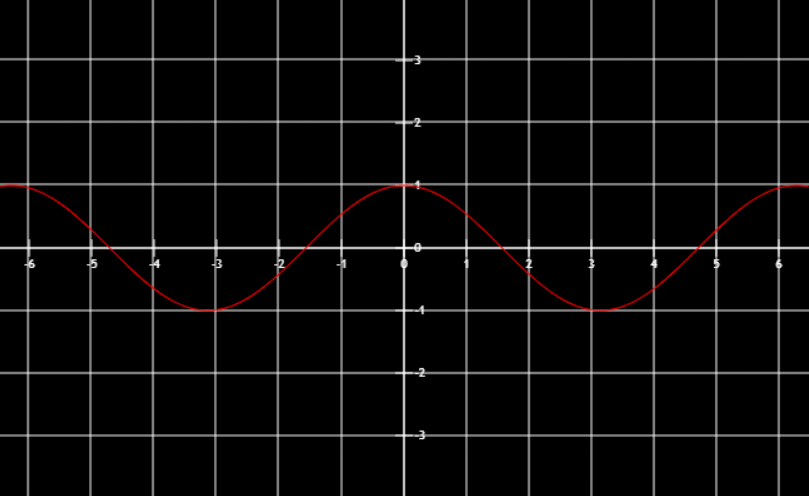
特殊值:
sin0=0 sin6π=21 sin4π=22 sin3π=23sin2π=1 sinπ=1 sin23π=−1 sin2π=0cos0=1 cos6π=23 cos4π=22 cos3π=21cos2π=0 cosπ=−1 cos23π=0 cos2π=1
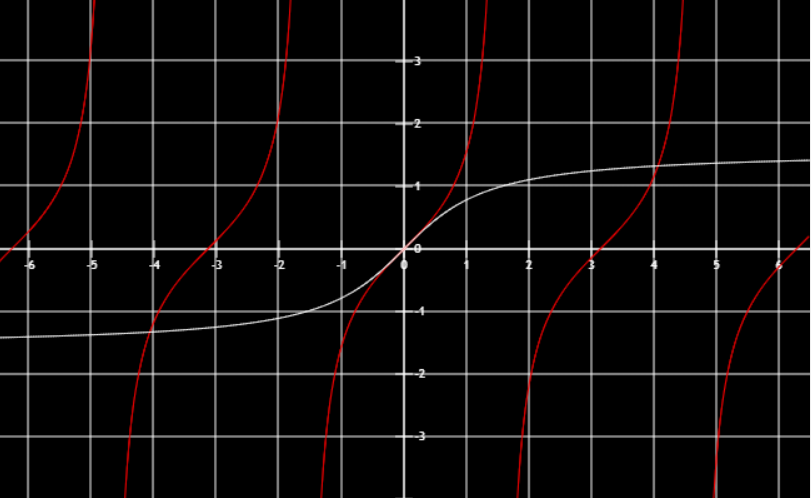
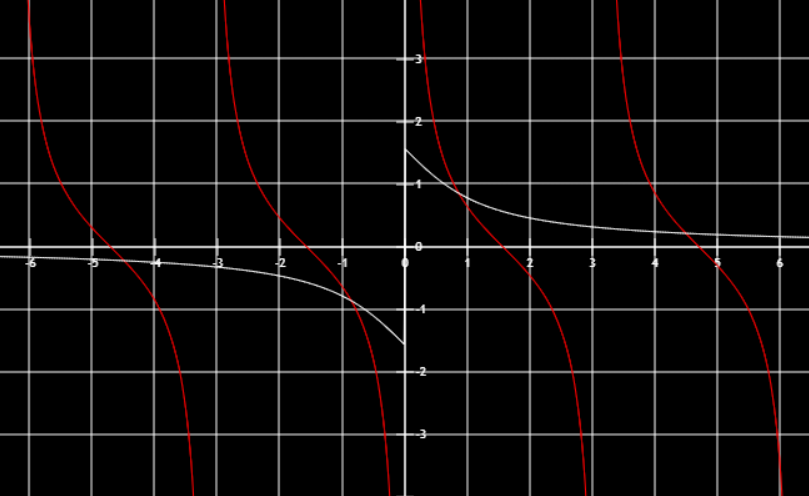
特殊值
tan0=0 tan6π=33 tan4π=1 tan3π=3lim2πtanx=∞ tanπ=0 limx3πtanx=∞ tan2π−0lim0cotx=∞ cot6π=3 cot4π=1 cot3π=33cot2π=∞ limπcotx=∞ cot23π=∞ lim2πcotx=∞
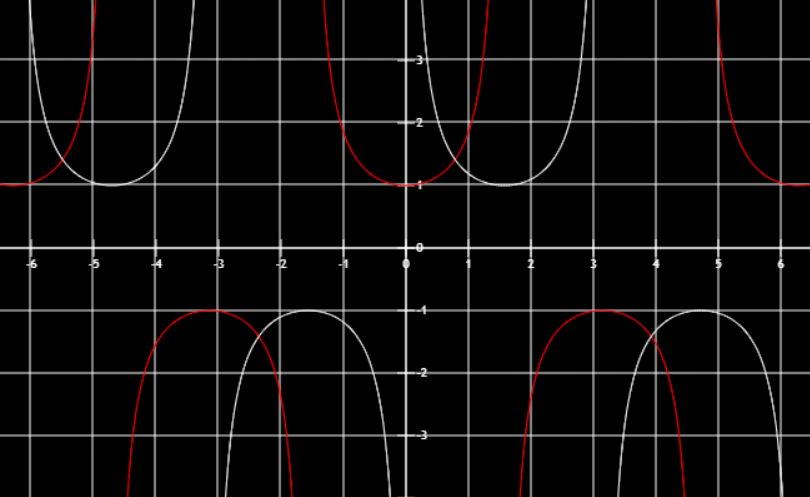
secx=cosx1,cscx=sinx1,取倒数画图
特殊值
arcsin0=0 arcsin21=6π arcsin22=4π arcsin23=3π arcsin1=2πarccos1=0 arccos23=6π arccos22=4π arccos21=3π arccos0=2π
分段函数
y∣x∣={x,x≥0−x,x<0
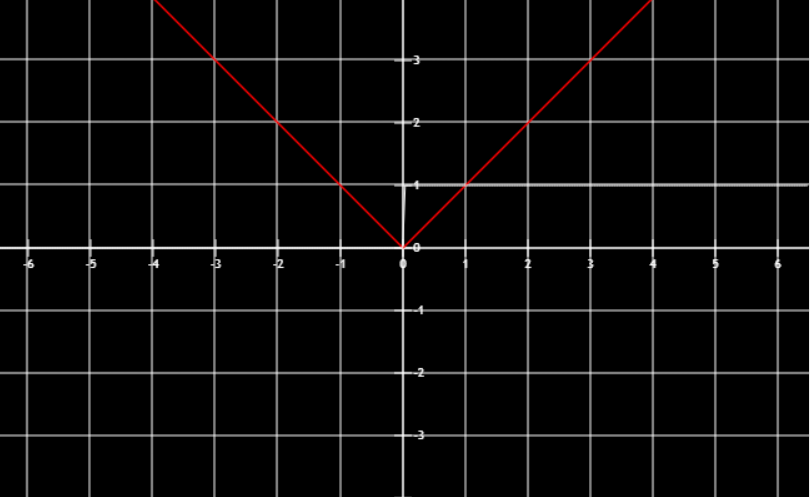
y=sgnx=⎩⎪⎨⎪⎧1,x>0x,x=0−1,x<0
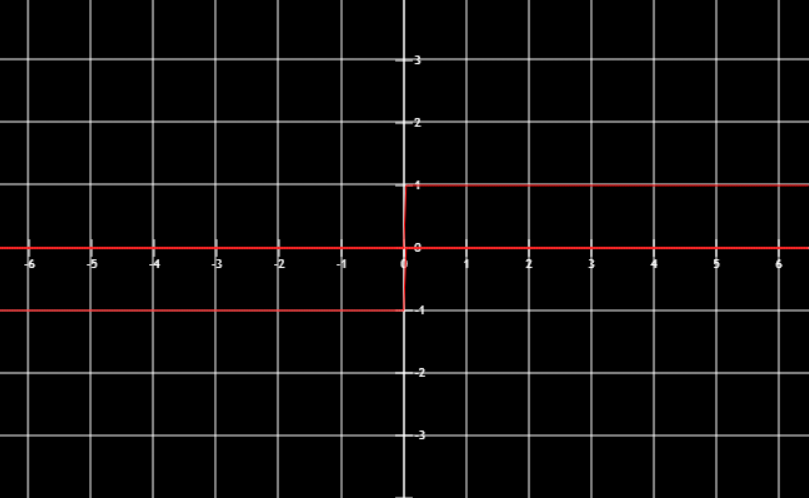
取整函数
向下取整,[0.99]=0,[-0.99]=-1
x−1<[x]≤xlimo+=0,lim0−=1
![[x]](https://cdn.jsdelivr.net/gh/Blosslom1/img@master/math/advanced_math/18.PNG)
向上取整,[0.99]=1,[-0.99]=0
x<[x]≤x+1limo+=1,lim0−=0
![[x]](https://cdn.jsdelivr.net/gh/Blosslom1/img@master/math/advanced_math/19.PNG)
图像变换
平移
平移变换
左加右减
f(x+x0)左平移,f(x-x0)右平移
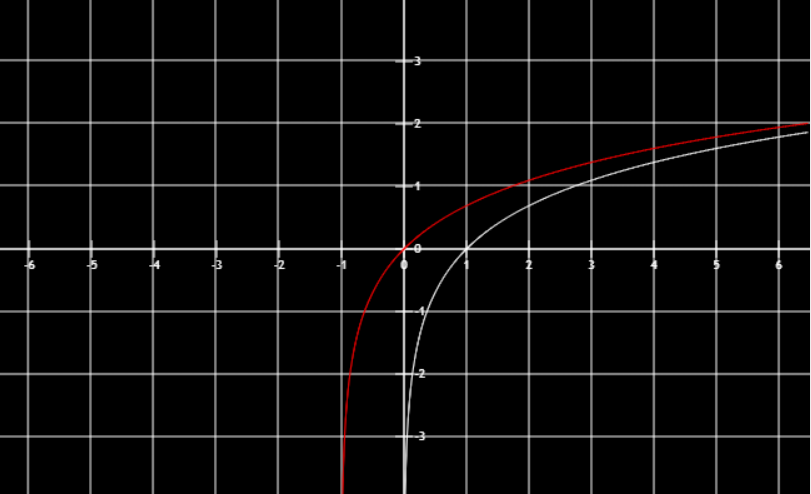
上加下减
f(x)+y上平移,f(x)-y下平移
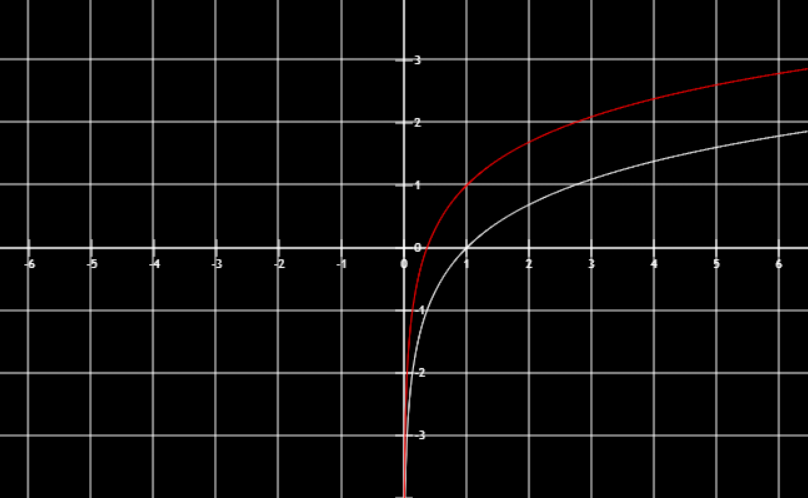
对称变换
-f(x)关于x轴对称
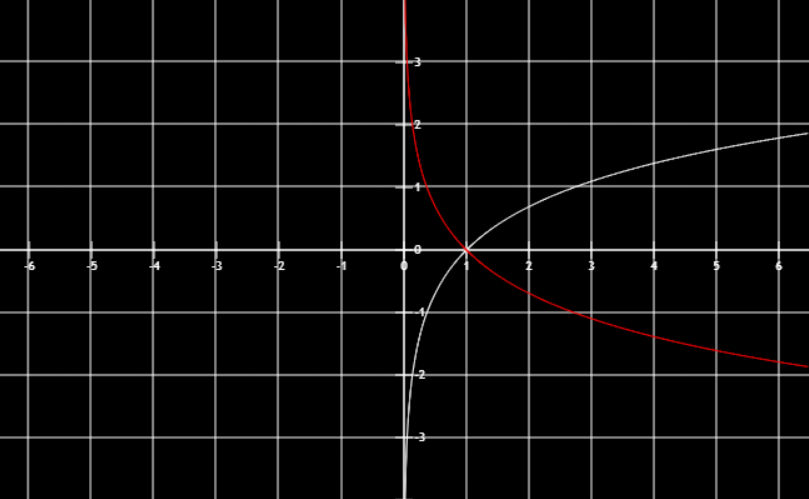
f(-x)关于y轴对称
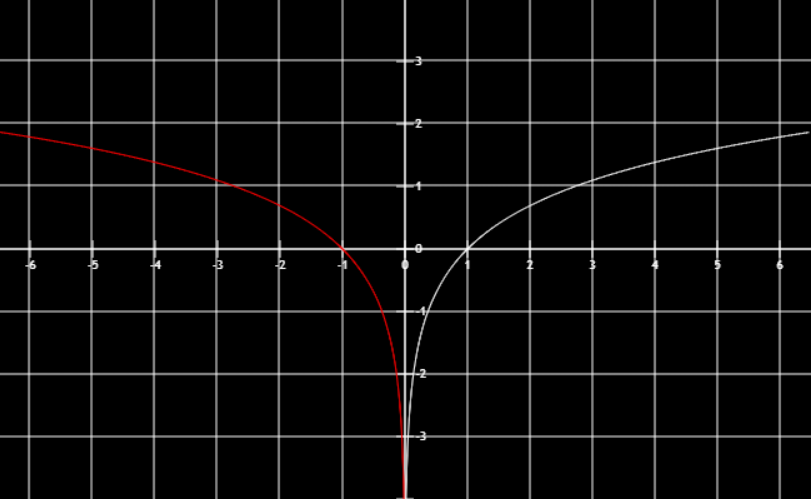
|f(x)|x轴下方的部分去掉关于x对称
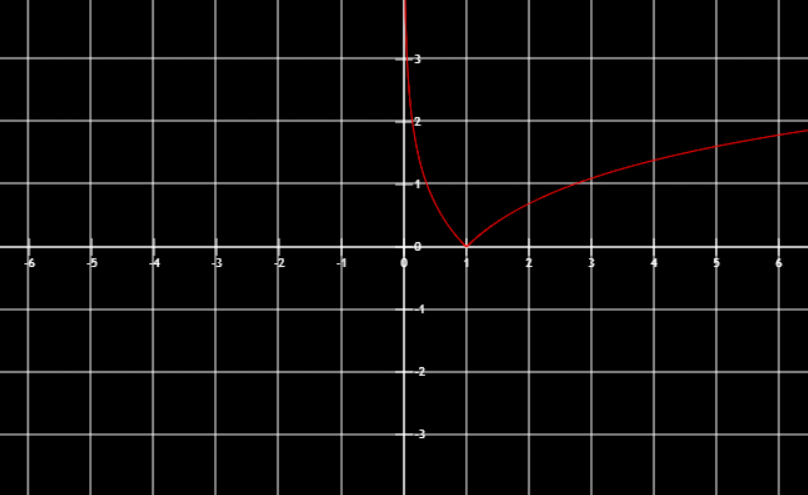
f(|x|)y轴左方的部分去掉关于y对称
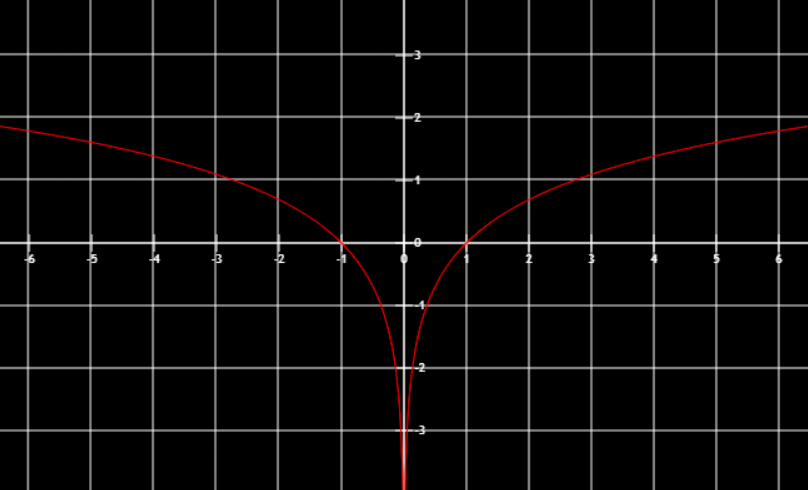
伸缩变换
f(kx)当k>1缩短到原来的1/k
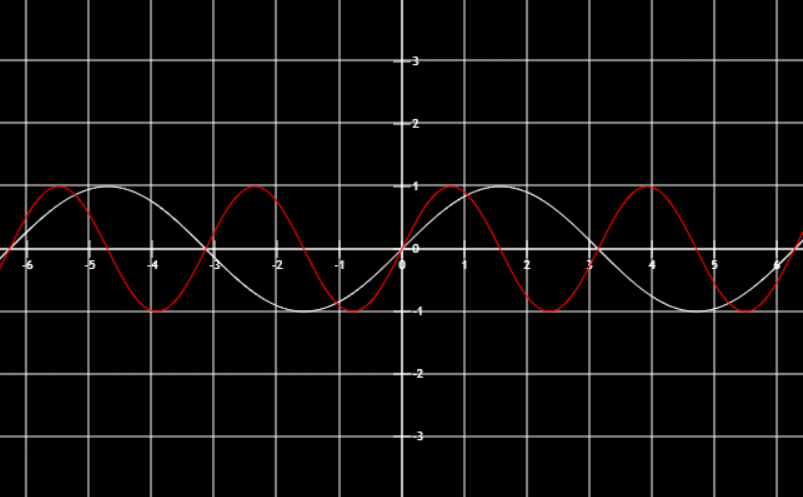
f(kx)当0<k<1身长的原来的1/k
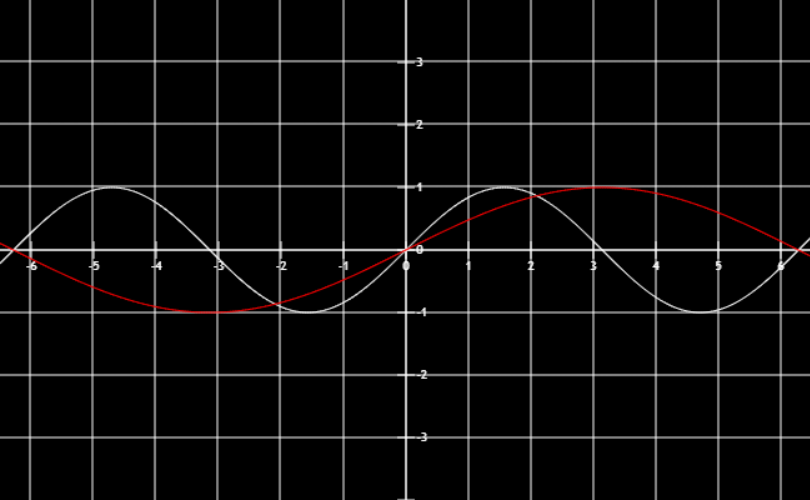
kf(x)y轴方向增加k倍
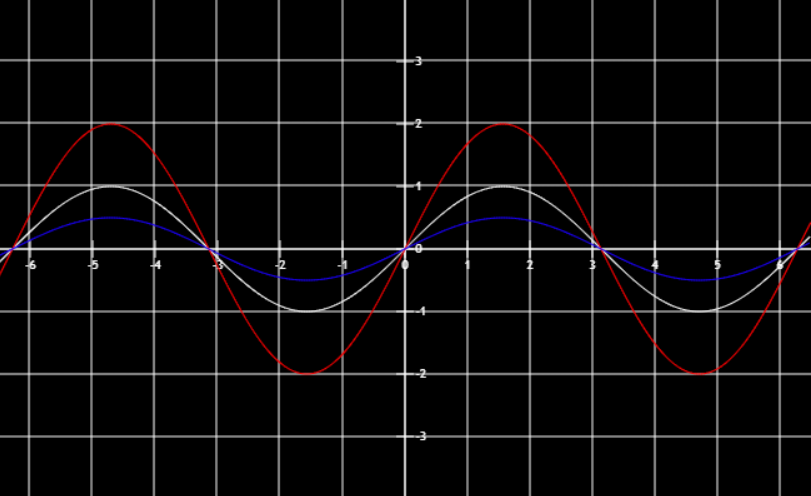
极坐标系
心形线(外摆线)
r=a(1−cosθ)(a>0)
画图描点
θ 0 12π 4π r 0 a2−3 22−2a
图像
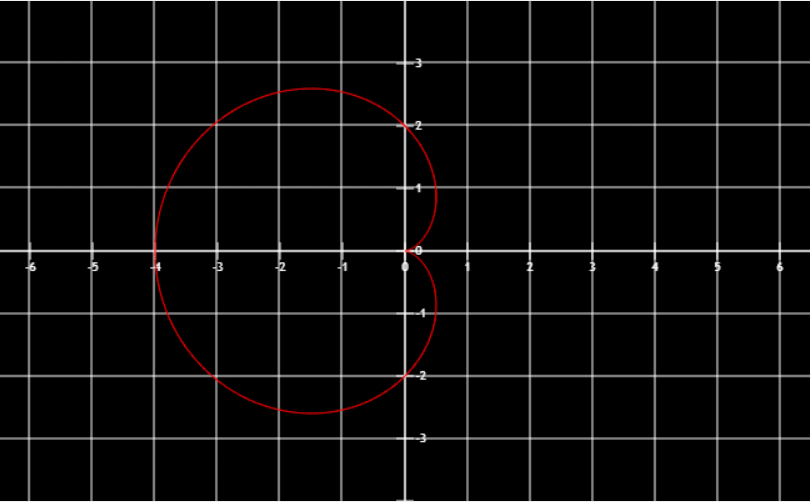
2(1−cosθ)
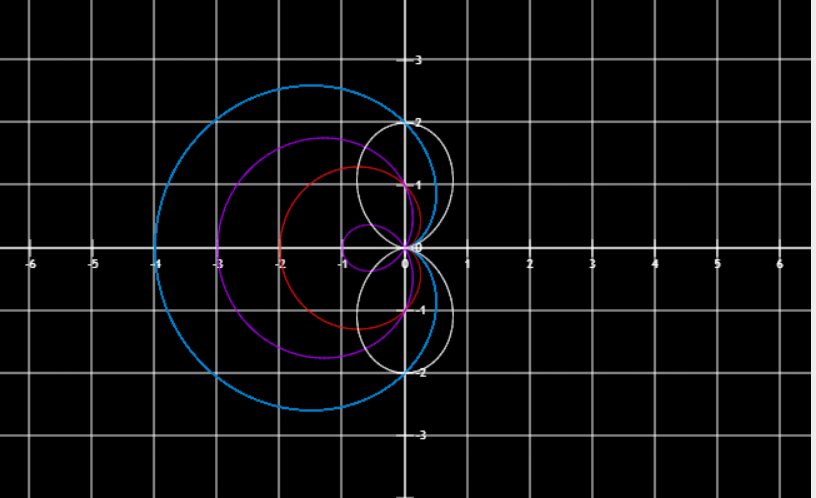
蓝2(1−cosθ)红1−cosθ紫1−2cosθ白1−cos2θ
玫瑰线
r=asinθ(a>0)
画图使用描点法
θ 0 12π 6π 4π 3π 125π 2π 127π 32πr 0 22a a 22a 0 −22a −a −22a 0
图像变换
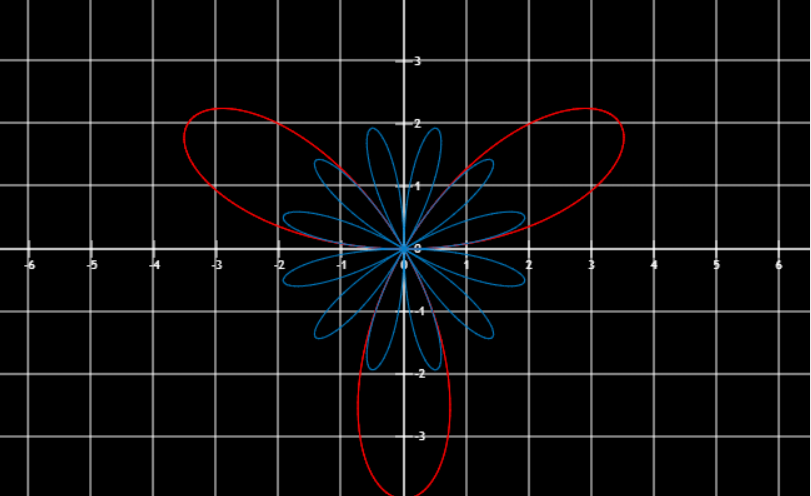
红r=4sin(3θ),蓝r=2sin(6θ)
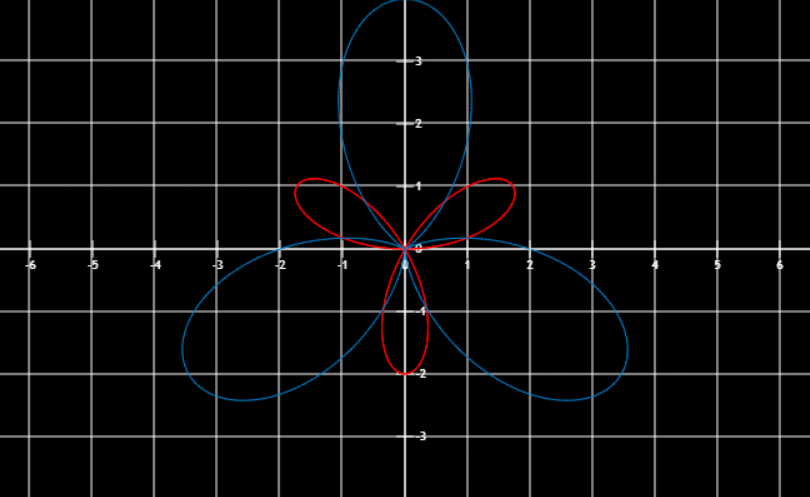
红r=2sin(3θ),蓝r=2(1−sin(3θ))
阿基米德螺线
r=aθ(a>,0,θ≥0)
图像
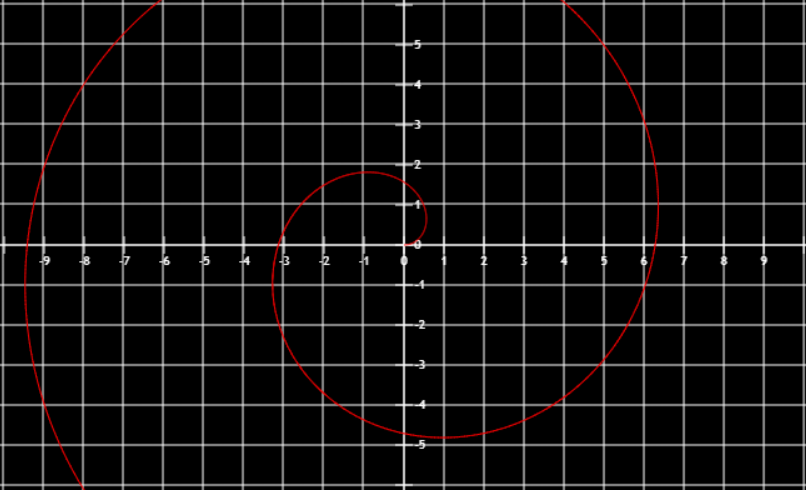
r=θ,(0<θ<6π)
伯努利双纽线
r2=a2cos2θ
画图
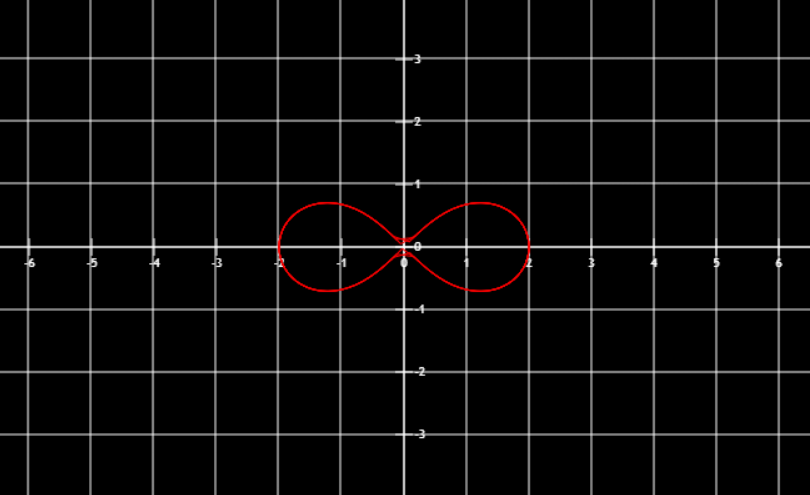
r2=22cos2θ
直角坐标系法
将极坐标的表达式使用基本方程的方法画出图像,再转化为极坐标图像
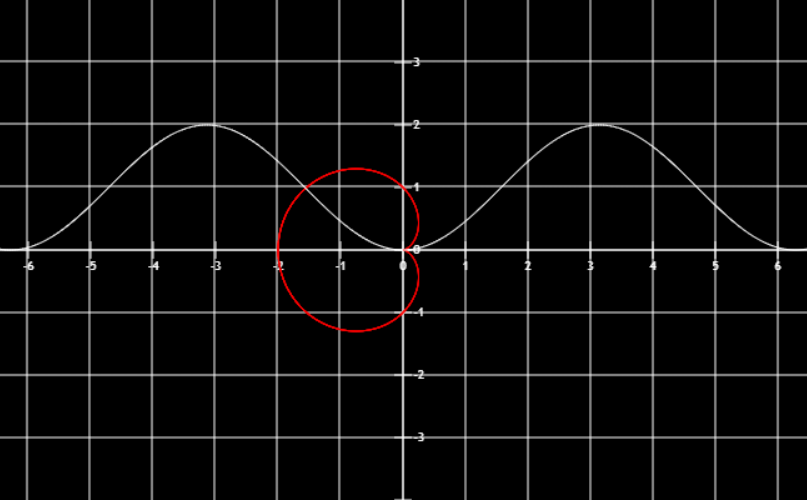
r=1−cosθ
对数螺线
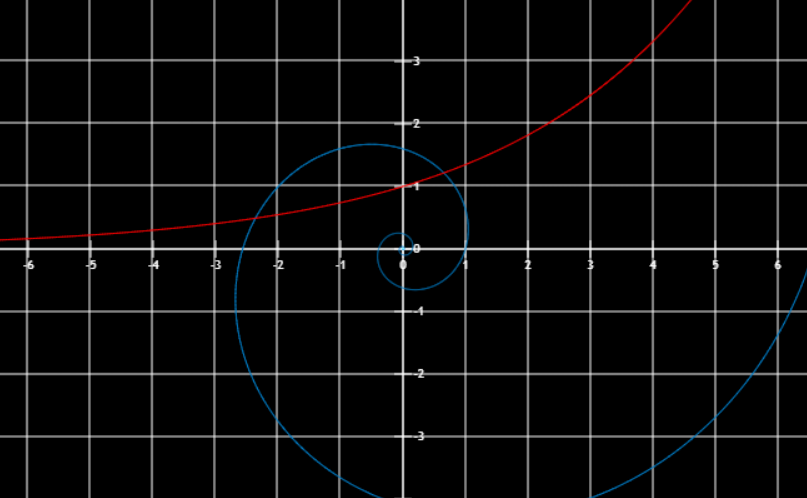
r=e0.3θ
参数方程
摆线(平摆线)
{x=r(1−sint)y=r(1−cost)
图像
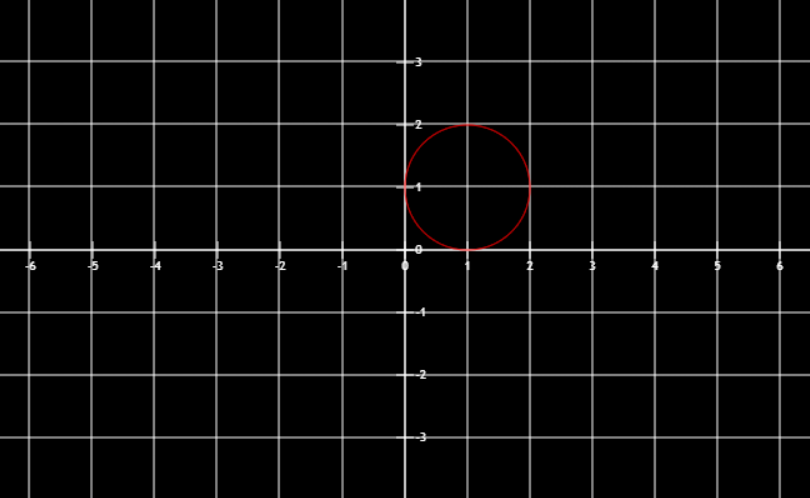
{x=1−sinty=1−cost
星形线(内摆线)
{x=rsin3ty=rcos3t消去t的直角坐标方程:x32+y32=r32
图像
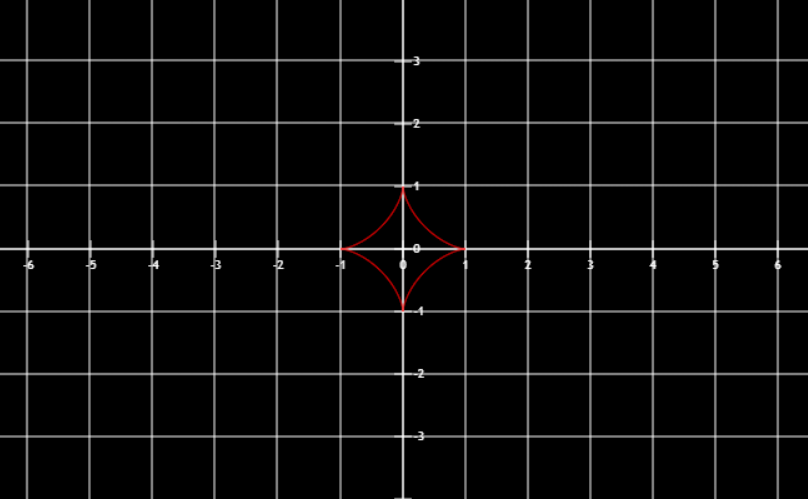
{x=sin3ty=cos3t
数列
等差数列
首项为a1,公差为d(d=0),a1,a1+d,a1+2d,...,a1+(n−1)d,...通项:an=a1+(n−1)d前n项和:Sn=2n[2a1+(n−1)d]=2n(a1+an)
等比数列
首项为a1,公比为r(r=0),a1,a1r,a1r2,...,a1rn−1,...通项:an=a1rn−1前n项和Sn={na1,r=11−ra1(1−rn),r=1常用1+r+r2...+rn−1=1−r1−rn,(r=1)
常见数列
12+22+32+...+n2=6n(n+1)(2n+1)1×21+2×31+3×41+...+n×(n+1)1=n+1n
裂项相消
1+1⋅21+2⋅31...+n⋅(n+1)1=1+11−21+21−31+...+n1−n+11=2−n−11
三角函数
三角函数表
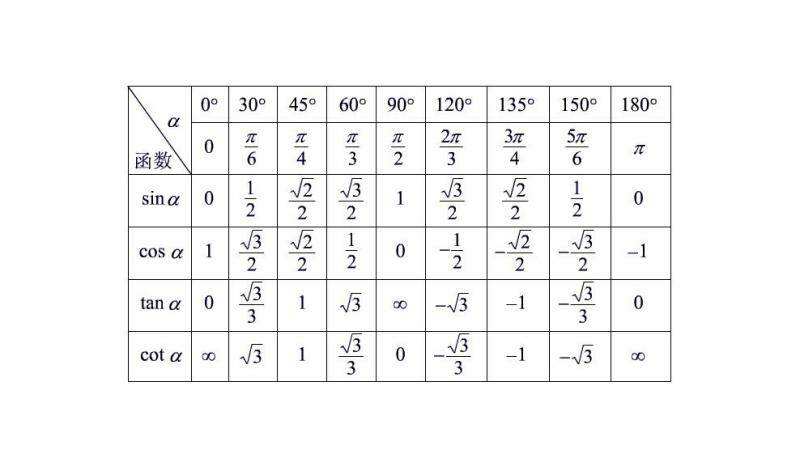
诱导变换
sin(2π±α)=cosαcos(2π±α)=∓sinαsin(π±α)=∓sinαcos(π±α)=−cosα奇变偶不变,符号看象限,2kπ奇偶看k,看前面的象限符号
关系式
cscα=sinα1,secα=cosα1,cotα=tanα1,tanα=cosαsinα,cotα=sinαcosαsin2α+cos2α=1,1+tan2α=sec2α,1+cotα=csc2α
和差公式
sin(α±β)=sinαcosβ±cosαsinβcos(α±β)=cosαcosβ∓sinαsinβtan(α±β)=1∓tanαtanβtanα±tanβtan(α±β)=cotα±cotβcotαcotβ∓1
倍角公式
sin2α=2sinαcosα,cos2α=cos2α−sin2α=1−2sin2α=2cos2α−1sin3α=−4sin3α+3sinα,cos3α=4cos3α−3cosαtan2α=1−tan2α2tanα,cot2α=2cotαcot2α−1
半角公式
sin22α=21(1−cosα),cos22α=21(1+cosα)sin2α=±21−cosα,cos2α=±21+cosαtan2α=sinα1−cosα=1+cosαsinα=±1+cosα1−cosαcot2α=1−cosαsinα=sinα1+cosα=±1−cosα1+cosα
积化和差公式
sinαcosβ=21[sin(α+β)+sin(α−β)]cosαsinβ=21[sin(α+β)−sin(α−β)]cosαcosβ=21[cos(α+β)+cos(α−β)]sinαsinβ=21[cos(α−β)−cos(α+β)]
和差化积公式
sinα+sinβ=2sin2α+βcos2α−βsinα−sinβ=2sin2α−βcos2α+βcosα+cosβ=2cos2α+βcos2α−βsinα−cosβ=−2sin2α+βsin2α−β
万能公式
若u=tan2x(−π<x<π),则sinx=1+u22u,cosx=1+u21−u2
导数
导数严格大于零,函数严格单调增,必有反函数
基本求导公式
C′=0(xu)′=uxu−1(tanx)′=(secx)2(cotx)′=−(cscx)2(secx)′=secxtanx(cscx)′=−cscxcotx(ln∣x∣)′=x1logax=alnx1(ln(x+x2+1))′=x2+11 (arcsinx)′=1−x21(arccosx)′=−1−x21(arctanx)′=1+x21(arccotx)′=−1+x21
基本积分表
∫x2+a21dx=ln(x+x2+a2)+C
极限
无限趋近的过程
n→∞limn+1n=1
证明上面数列第n项:
第n项与1之间的距离如下
∣n+1n−1∣=n+11让距离在(0,ϵ),n+11<ϵ则n>ϵ1−1从数列第N项开始,N>ϵ1−1都会保持与1的距离小于ϵ∣n+1n−1∣<ϵ
三步证明
∣xn−a∣<ϵ反解出n>g(ϵ)取N=[g(ϵ)]+1 (意思是取整后加1)(n>N)
例题:
定义证明n→∞lim[1+n(−1)n]=1证:(1)距离∣1+n(−1)n−1∣<ϵ(2)n1<ϵ反解n>ϵ1(3)取N=[ϵ1]+1故当n>N时,n>ϵ1使∣1+n(−1)n−1∣<ϵ
数列极限定义
一数列,有常数a,对于任意ϵ>0,总有N,当n>N时|数列-a|<ϵ,则a是数列的极限,或数列收敛与a
如果没有a则数列是发散的
n→∞limxn=1或xn−>a(n−>∞)常用语言ϵ−N:n→∞limxn=a,∀ϵ>0,∃N>0,当n>N时,衡有∣xn−a∣<ϵ
∀是Arbitrary,∃是Exists
例题:
证明:若n→∞liman=A,则n→∞lim∣an∣=∣A∣证,∀ϵ>0,∃N>0,当n>N时,∣an−A∣<ϵ由不等式∣∣a∣−∣b∣∣≤∣a−b∣∣∣an∣−∣A∣∣≤∣an−A∣<ϵ所以n→∞lim∣an∣=∣A∣成立倒着推不一定成立,因为极限的唯一性
拓展
n→∞liman=0<=>n→∞lim∣an∣=0夹逼准则使用绝对值可以省去证明后面的
子数列
子数列来自数列,将偶数或奇数项变成子数列
- 如果数列收敛,其任何子数列都收敛
- 但凡有一个子数列发散,数列就发散
- 如果俩个子数列收敛值不同,则数列就发散
性质
定理1:唯一性,给出极限时唯一的
定理2:有界性,极限有界
定理3:保号性,去掉lim的帽子符号保持不变(脱帽法)
n→∞liman=a>0=>an>0(n>N)
保号性拓展(戴帽法),一定要带等号
an>0,且n→∞liman=aa≥0
极限运算规则
若:n→∞limxn=a,n→∞limyn=b则(1)n→∞lim(xn±yn)=a±b(2)n→∞limxnyn=ab(3)b=0,yn=0n→∞limynxn=ba
例题
设n→∞lim(an+bn)=1,n→∞lim(an−bn)=3,证{an}{bn}存在并求值{un=an+bn,limn→∞un=1mn=an−bn,limn→∞mn=3n→∞lim(un+mn)=n→∞lim2xn=2n→∞limxn=4n→∞liman=2n→∞lim(un−mn)同理n→∞limbn=−1
误区
上面的题目容易直接使用法则运算n→∞lim(an+bn)=n→∞liman+n→∞limbn其实不确定n→∞liman或bn是否存在如果an=(−1)n,bn=−(−1)n+1极限都不存在
夹逼准则
如果数列{yn}{xn}{zn}满足下列条件yn<x≤zn;n→∞limyn=a,n→∞limzn=a则n→∞limxn=a
不纠结等号
例题
求极限n→∞lim(n2+1n+n2+2n+...+n2+nn)n2+nn2<i=1∑nn2+in<n2+1n2n→∞limn2+1n2=1n→∞limn2+nn2=1即i=1∑nn2+in=1所以n→∞lim(n2+1n+n2+2n+...+n2+nn)=1
单调有界准则
单调有界数列必有极限
见到递推式an+1=f(an),一般用这个
例题
设数列{xn}满足0<x1<π,xn+1=sinxn,证明n→∞limxn存在并求该极限证:n取1时,x2=sinx1根据不等式sinx1<x1设xn=sinxn−1<xn−1,x2<x1可推出xn<x1所以0<xn+1=sinxn<π故xn单调递减有下界0=>n→∞limxn存在记为A=>A=sinA=>A=0n→∞limxn=0
函数极限
邻域
以点x为中心的任何开区间称为x的邻域,去心邻域是不包括x
函数极限定义
设函数f(x)在点x0的某一去心邻域有定义,若存在常数A,对任意给定的ϵ,总有正数δ使得0<|x-x0|<δ时,f(x)满足|f(x)-A|<ϵ,A是f(x)当x->x0时的极限
x→x0limf(x)=A或f(x)−>A(x−>x0)常用语言ϵ−δ:x→x0limf(x)=A,∀ϵ>0,∃δ>0,当0<∣x−x0∣<δ时,衡有∣f(x)−A∣<ϵ常用语言ϵ−X:x→∞limf(x)=A,∀ϵ>0,∃X>0,当∣x∣>X时,衡有∣f(x)−A∣<ϵ
单侧极限
左极限x→x0−limf(x)=A或f(x0−)右极限x→x0+limf(x)=A或f(x0+)充要条件x→x0limf(x)=A<=>n→x0−limf(x),且x→x0+limf(x)
函数极限性质
唯一性
局部有界性
x→x0limf(x)=A则有正常数M和δ,当0<∣x−x0∣<δ,有∣f(x)∣≤Mx→x0limf(x)=A=>∣f(x)∣≤M,不能反推f(x)在[a,b]上连续,f(x)在[a,b]上有界有界函数和有界函数的和,差,积仍是有界函数(有限个)若f′(x)在有限区间(a,b)内有界,则f(x)在该区间内有界
局部保号性
若x→x0limf(x)=A>0,则x−>x0时,f(x)>0limf(x)=1,意思是不管多大区间f(x)都待在1旁边
脱帽法:
x→x0limf(x)=A<=>f(x)=A+α(x),x→x0limα(x)=0
戴帽法:
若f(x)≥0,且x→x0limf(x)=AA≥0
自变量取值的双向性,因为极限的唯一性所以两个值的都不存在,遇到指数函数,绝对值,反三角函数,取整函数,都要分开讨论。
x→∞limex,x→−∞limex=0,x→+∞limex=+∞,所以不∃x→0lim∣x∣sinx,x→0+limxsinx=1,x→0−lim−xsinx=−1,所以不∃x→∞limarctanx,x→−∞limarctanx=−2π,x→+∞limarctanx=+2π,所以不∃x→0lim[x],x→0+lim[x]=0,x→0−lim[x]=−1,所以不∃
例题
设a为常数,且x→0lim(ex2+1ex1−π+a⋅arctanx1)存在,求a的值,并计算极限。解:极限中有指数所以有双向性x→0+lim(ex2+1ex1−π+a⋅arctanx1)看次数最大的比值=x→0lim(e(x1)2+10⋅e(x1)2+1+ex1−π+a⋅arctanx1)=10+a⋅2π=2πax→0−lim(ex2+1ex1−π+a⋅arctanx1)=1−π+a⋅−2π=−π+−2πa因为极限存在所以唯一2πa=−π+−2πaa=−1x→0lim(ex2+1ex1−π+a⋅arctanx1)=−2π
极限运算规则
若limf(x)=A,limgx()=B,那么lim[kf(x)±lg(x)]=klimf(x)±llimg(x)=kA±lB,(k,l为常数)lim[f(x)⋅g(x)]=limf(x)⋅limg(x)=A⋅Blim[f(x)]n=[limf(x)]n,(n为正整数)limg(x)f(x)=limg(x)limf(x)=BA,(B=0)
夹逼准则
如果函数f(x),g(x)好人h(x)满足g(x)≤f(x)≤h(x)limg(x)=A,limh(x)=A则limf(x)存在,且limf(x)=A
洛必达法则
当x→a/∞limF′(x)f′(x)是00型即f′(x)F′(x)都是0且F′(x)=0,x→a/∞limF′(x)f′(x)存在或无穷大则F′(x)=0,x→a/∞limF(x)f(x)=x→a/∞limF′(x)f′(x)
当x→a/∞limF′(x)f′(x)是∞∞型即f′(x)F′(x)都是0且F′(x)=0,x→a/∞limF′(x)f′(x)存在或无穷大则F′(x)=0,x→a/∞limF(x)f(x)=x→a/∞limF′(x)f′(x)
泰勒公式
sinx=x−3!x3+o(x3), cosx=1−2!x2+4!x4+o(x4)arcsinx=x+3!x3+o(x3), tanx=x+3x3+o(x3)arctanx=x−3x3+o(x3), ln(1+x)=x−2x2+3x3+o(x3)ex=1+x+2!x2+3!x3+o(x3), (1+x)α=1+αx+2!α(α−1)x2+o(x2)
狗−sin狗=61狗3
无穷小运算规则
- 有限个无穷小的和是无穷小
- 有界函数数与无穷小的乘积是无穷小
- 有限个无穷小的乘积是无穷小
o(xm)±o(xn)=o(xmin{m,n})(加减法低阶吸收高阶)o(xm)⋅o(xn)=o(xm+n)/xm⋅o(xn)=o(xm+n)(乘法阶乘累加)o(xm)=o(kxm)=ko(xm)k=0(非零常数相乘不影响)
A/B型,适用于上下同阶原则,把分子分母展开到相同的次幂
A-B型,幂次最低原则,可以转化为A+(-B),A和B分别展开到他们的系数不相等的x的最低次幂为止
题目一
x−>0,求x−sinxsinx=1⋅x1−61x3+o(x3)x−sinx=61x3+o(x3)x−sin−>61x3
题目二
x−>0,求x+sinxx−(−sinx)−sinx=−1⋅xx−(−sinx)=2x+o(x)x+sinx=2x
常用等价无穷小
x−>0sinx−>x,tanx−>x,arcsinx−>x,arctanx−>x,ln(1+x)−>xex−1−>x,ax−1−>xlna,1−cosx−>21,(1+x)α−>1αx,xlnx−>0x→1limlnx=(x−1)使用等价代换sing(x)−>g(x)则sinx3−>x3
无穷大无穷小都只是一个过程,任何数都不会是无穷大,如果f(x)为无穷大,则1/f(x)是无穷小
若limβ(x)α(x)=00=0,则α(x)是比β(x)高阶无穷小,α(x)=o(β(x))若limβ(x)α(x)=00=∞,则α(x)是比β(x)低阶无穷小若limβ(x)α(x)=c=0,则α(x)与β(x)同阶无穷小若limβ(x)α(x)=1,则α(x)与β(x)等价无穷小,α(x)−β(x)若lim[β(x)]kα(x)=c=0,则α(x)是β(x)k阶无穷小
未定式
00=∞∞0⋅∞={∞1⋅∞=∞∞0⋅01=00设置分母简单因式(xα,ex)才下方,形成不稳定三角形。∞−∞和差化积∞0,00,1∞=>uv=evlnu=⎩⎪⎨⎪⎧∞0−>e0⋅∞00−>e0⋅∞1∞−>e∞⋅0
归结原则
设f(x)在U(x_0,\delta)内有定义\\
则\lim_{x \to x_0}f(x)=A存在<=>对任何U(x_0,\delta)内以x_0为极限的数列\{xn\},极限\lim_{x \to \infty}=A存在\\
\lim_{x \to x_0}f(x)=A存在<=>\lim_{x \to \infty}=A存在\
题目一
x→0limx100e−x21不能使用洛必达,头轻脚重,换成到三角形x−2=t,则t→0lim=t−50e−t=ett50洛必达=et0=0
题目二
x→−∞limx(x2+100+x)=xx2+100−xx2+100−x2=x2+100−x100xx=−t.则x→+∞lim=x2+100−x−100x=1+x2100+1−100=−50
题目三
x→0+limxlnx=x−1lnx洛必达=x−2x−1=x=>0
题目四
x→1−limlnxln(1−x)画图=(1−x)ln(1−x)t=(1−x),则t→0+limtlnt=0⋅−∞=0
题目五
x→0limsinx−tanxarcsinx−arctanx泰勒=x−6x3+o(x3)−[x+3x3+o(x3)]x+6x3+o(x3)−[x−3x3+o(x3)]=2x3−2x3=3−1
函数连续与间断
连续点
函数在某去心邻域有定义
函数f(x)在点x0的某一邻域内有定义,且有x→xolim=f(x0),则函数有在x0处连续
间断点
函数在某去心邻域有定义
**可去间断点:**极限有定义且函数存在(或函数无定义)但是两者不等。可以补充定义使得连续,故又叫可补间断点
**跳跃间断点:**左极限和右极限都存在但不等故极限不存在,称为跳跃间断点
无穷间断点
若x→x0limf(x)=∞,则这类间断点称为无穷间断点,如函数y=x1,点x=0处为无穷间断点。
振荡间断点
若若x→x0limf(x)震荡不存在,称这类间断点为振荡间断点,如y=sinx1,x=0无定义
题目一
讨论间断点看两类点
设函数f(x)=∣x−1∣ln∣x∣sinx,则f(x)间断点是x=1,x=0时无定义f(1)不存在f(0)不存在x→1lim∣x−1∣lnxsinx={x→1+→sin1x→1−→−sin1x=1是跳跃间断点x→0lim1ln∣x∣⋅sinxx→0limxlnx=0x=0是可去间断点
拉格朗日中值定理
f(b)−f(a)=f′(ξ)(b−a)
其他公式
极限变换公式
(1),ef(x)−eg(x)=eg(x)[ef(x)−g(x)−1]等价f(x)−g(x)
华里士公式
∫02πsin6xdx=65⋅43⋅21⋅2π∫02πcos5xdx=54⋅32


















![[x]](https://cdn.jsdelivr.net/gh/Blosslom1/img@master/math/advanced_math/18.PNG)
![[x]](https://cdn.jsdelivr.net/gh/Blosslom1/img@master/math/advanced_math/19.PNG)




















