高分子化学
基本概念:
单体:
能够形成高分子化合物的小分子化合物。
烯烃,含有官能团的化合物,环状化合物。
高分子化合物(polymer):
有多种原子通过共价键连接而成的分子质量很大的化合物。
| ~1000 |
103~104 |
104~106 |
106~ |
| 小分子 |
齐聚物,低聚物 |
聚合物,高聚物,大分子 |
超高分子量聚合物 |
多种原子组成,C,H,O,N,S,Cl,P,Si
术语:
结构单元:
一种单体聚合进入聚合物链的部分
重复单元(链节):
高分子链中可重复的最小单元
单体单元:
与单体组成相同,只是电子结构不同的重复单元
关系:
结构单元=重复单元(链节)=单体单元:正常的加聚
DP=Xn=n
结构单元=重复单元(链节)≠单体单元:脱去一分子水
DP=Xn=n
结构单元1+结构单元2=重复单元=链节 没有单体单元:两种分子脱去一分子水
2DP=Xn=2n
——[——重复单元化学式——]n——
聚合度:(衡量高分子大小的一个指标)下面为表示方法
平均聚合度(n):聚合物分子量大小的指标
重复单元的数目,记做
DP
结构单元的数目,记做
Xn
可以算出分子量(M0是结构单元分子量)
M=Xn×M0=DP×M0 or 2DP×M0
主链:
尺寸最大,惯穿整个大分子的分子链
侧基:
在主链除H以外的原子或原子团
端基:
聚合物末端的基团
侧链:
侧基足够长时叫测链
聚合物命名
- 碳链聚合物:主链全部是C
- 杂链聚合物:除了C还有其他
- 元素有机聚合物:主链没有C
-
按照源基础命名:聚+单体名称
-
按聚合物结构特征命名:
-
按照习惯命名:
加成聚合与缩合聚合
- 加成聚合(加成反应,连锁聚合的反应机理)
- 缩合聚合(缩聚反应,逐步聚合的反应机理)
- 开环聚合
链式聚合与逐步聚合(Flory分类)
链式聚合(连锁聚合)
有多种基元反应 链引发=>链增长=>链终止
有特定的活性中心
一个分子链瞬间形成
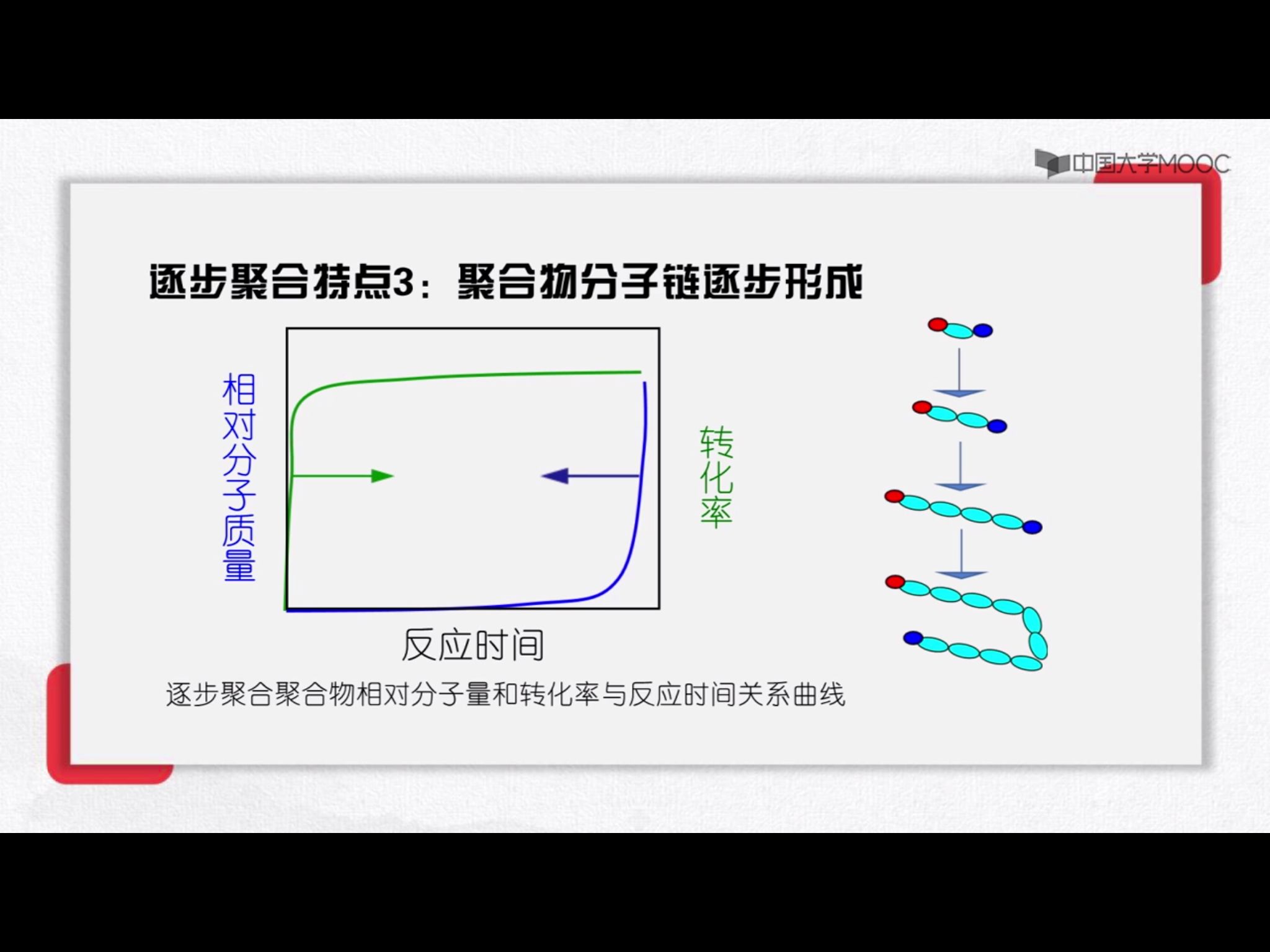
逐步聚合
没有特定的活性中心
单一基元反应
逐步形成

HDPE高密度聚乙烯,PET聚对苯二甲酸乙二醇酯,PVC聚氯乙烯,LDPE低密度聚乙烯,
PP聚丙烯,PS聚苯乙烯
分子量及分布
数均分子量:所有分子重量除以分子摩尔总数(m分子总重量,n分子数,M分子量,x分子分率)
按照分子数目统计
m:所有体系总质量 mi:单个体系质量 Mi:单个体系分子量 ni:单个体系分子数量Mn=Σnim=ΣniΣniMi=Σ(Mimi)Σmi=ΣxiMi
统计方法:
- 冰点降低法
- 沸点升高法
- 渗透压法
- 蒸汽压法
- 端基滴定法
重均分子量:分子量乘以重量分数的加和(w质量分率)
按照重量统计
Mw=ΣmiΣ(miMi)=Σ(niMi)Σ(niMi2)=Σ(wiMi)
上述两种分子量可以使用凝胶渗透法测得
粘均分子量:溶剂体系,特性粘度
η=KMα K,α是常数 α 一般在0.5−0.9MV=[ΣmiΣ(miMiα)]α1=[Σ(niMi)Σ(niMiα+1)]α1
分子量分布
Mn<Mv<Mw,数均分子量受低分子量影响,重均分子量受高分子量影响
多分散性:分子量大小不一,参差不齐的特性
重均分子量和数均分子量的比值
| Mw/Mn |
分子量分布情况 |
| 1 |
均一分部 |
| 1.5~2 |
分布较窄 |
| 20~50 |
分布较宽 |
大分子微结构
序列结构:
首尾相连 首首相连 尾尾相连
手性结构:
等规立构 间规立构 无规立构
几何构型:
3,4加成 1,2加成 反式1,4加成 顺式1,4加成
几何形状:
线性高分子:可溶可熔
支链型高分子:可溶可熔
交联型高分子:不熔不溶
凝聚态和热转变
玻璃态=>玻璃化转变区域=>橡胶态(高弹态)=>黏弹态转变区域=>黏流态
缩聚和逐步聚合
缩聚反应
有低分子副产物
缩聚物和单体分子量不成正比
-
1-1,1-2官能度体系只能得到低分子化合物
-
2-2,2官能度体系可以形成线性缩聚物
-
2-3,2-4等多官能团体系可以形成体形缩聚物
-
一分子能参加反应的官能团数叫官能度(f)
-
均缩聚:只有一种单体参加反应
-
杂缩聚:两种单体参加反应
-
共缩聚:两种以上单体参加反应
ABS:接枝共聚物,SBS:嵌段共聚物
无规,嵌段,节支,交替二元共聚物
-
那些物质可以进行自由基聚合?
绝大多数烯类单体
聚合方法:溶液,熔融,界面,固相缩聚
线性缩聚反应机理
- 参加反应的两个官能团形成大分子向两个方向增长
- 成环是副反应,五元环和六元环最稳定最容易形成,低浓度利于成环
反应程度(P):参加反应的官能团占起始官能团的分数
N0是起始官能团数,N是残留的官能团
P=N0N0−N=1−N0N
转化率:参加反应的单体量占起始单体量的分数
平均聚合度:
Xn=t时大分子数结构单元数目=NN0 Xn平均聚合度带入上面反应程度关系式P=1−Xn1
一般高分子若Xn=100~200 则 P=0.99~0.995
不可逆线性缩聚动力学
自催化缩聚反应(三级反应)
(1−P)21=2C02kt+1 P−t关系式Xn=1−P1 带入(Xn)2=2C02kt+1 Xn−t关系式
外加酸催化缩聚反应(二级反应)
1−P1=C0k、t+1 P−t关系式Xn=C0k、t+1
可逆线性缩聚动力学
封闭体系
dtdP=k1C0[(1−P)2−KP2] 水未排除时dtdP=k1C0[(1−P)2−KPnw] 水部分排除时nw小分子残留浓度
线性缩聚聚合度
影响因素:反应程度
通冷却可控制反应程度,反应程度限制条件可逆反应,原料非等当量比
平均聚合度,反应程度,平衡常数关系(封闭)
Xn=1−P1=K+1
| 聚酯化反应 |
K=4 |
P=0.67 |
Xn=3 |
| 聚酰胺反应 |
K=400 |
P=0.95 |
Xn=21 |
| 不可逆反应 |
K=104 |
P=0.99 |
Xn=101 |
平均聚合度,反应程度,平衡常数关系(部分排水)nw体系中残留水分C0没有就不用
Xn=1−P1=PnwKc0≈nwKc0P=>1,可以去掉P,Xn=nwKc0当c0=1,去掉c0,Xn=nwK
控制聚合度:
端基封锁:是某官能团稍过量,加入少量单官能团物质
Na Nb 分别是两个官能团起始数r=NbNa 摩尔系数(官能团数之比)q=2Na2(Nb−Na)=NaNb−Na=r1−r b的过量分率(分子数之比)r=q+11
Xn,P,r,q之间的关系
Xn=1+r−2rP1+r=q+2(1−P)q+2r=1,or,q=0原料单体等当量比P=1,官能团a完全反应
聚合度分布:
数均聚合度的推导
单个基团形成概率p,x−1个是px−1,最后一个不形成是1−p,所以形成x−聚体的概率是px−1(1−p)Nx是x−聚体分子,N是大分子总数Nx=Npx−1(1−p)由p=1−N0N得N=N0(1−p)Nx=N0px−1(1−p)2x聚体的质量分布函数WWx=N0xNx=xpx−1(1−p)2
数均聚合度,重均聚合度
数均聚合度 Xn=1−p1 重均聚合度 Xw=1−p1+p分子量分布宽度 XnXw=1+p≅2
体形缩聚和凝胶化
出现凝胶的瞬间反应程度叫凝胶点
平均官能度:混合单体中参加反应的平均每一单体分子带有的官能团数
f=ΣNΣfN
不过量集团数的两倍
carothers推测凝胶点
f平均官能度,pc凝胶点f=ΣNiΣNifip=N0f2(N0−N)p=f2(1−Xn1)Xn=2−pf2当Xn无穷大,pc=f2
凝胶点时的临界反应程度:(凝胶点Pc,开始出现凝胶瞬间的反应程度)
PC=f2
凝胶点预测
f=Na+Nb+Nc2(Nafa+Ncfc) 两种以上计算方法f是官能度f是平均官能度N分子数分子是非过量基团,分母是所有基团f带入PC=f2反应程度p⊂(0−1) p<PC不形成凝胶
| 凝胶点 |
Pc>1,不凝胶 |
Pc<1,凝胶 |
| 平均官能度 |
f<2,不凝胶 |
f>2,凝胶 |
Flory推测凝胶点
- 支化点:官能度大于2的单体(支化单元)
- 支化系数:一个支化点连接另一个支化点的几率
ρ是支化单元中A官能团占全部A的分数(支化分率)ρ=混合物中管能团A总数支化单元中官能团A数=NAfA+NcfcNcfcPc=[r+rρ(f−2)]211α 支化系数,f 支化单元的官能团数α=1−rPA2(1−ρ)rPA2ρ=r−PB2(1−ρ)PB2ρ
凝胶化控制:控制反应温度
聚合方法
- 熔融缩聚(单体和聚合产物在熔融状态下的聚合反应)
- 最简单的缩聚方法,只有少量单体和催化剂
- 反应温度高(200-300),不适合生产高熔点聚合物
- 反应时间长,时间长有利于提高缩聚物分子量
- 需要惰性气体避免氧化降解(N2,CO2)
- 聚合后期需要减压
- 反应完成,流出,制带,冷却,切粒
- 溶液缩聚(单体在溶剂中进行的聚合反应)
- 聚合温度低
- 反应和缓平稳,有利热交换
- 不需要高真空
- 制得的聚合物溶液,可直接用作胶黏剂等
- 界面缩聚(两种单体熔于两种互不相容的溶剂,在界面处进行缩聚反应)
- 单体活性高,反应快,104-105l/mol.s
- 对单体纯度要求不严
- 溶剂贵回收麻烦
- 固相缩聚(熔点以下进行缩聚反应)
- 反应速度慢,表观活性大,110~331kJ/mol
- 由扩散控制,分子量高,纯度高
|
熔融缩聚 |
溶液缩聚 |
界面缩聚 |
固相缩聚 |
| 优点 |
生产简单,成本低,产能高 |
降低所需温度,平稳易控 |
反应缓和,不可逆,单体要求不高 |
反应缓和,所需温度低 |
| 缺点 |
反应温度高,设备密封性高,小分子不易脱去 |
溶剂有毒,易燃,成本高 |
必须活性单体,不能精制 |
速度慢,小分子不易脱去,原料要求高 |
| 适用范围 |
大品种缩聚物,聚酯,聚酰胺等 |
单体后缩聚物熔融后易分解的,芳香族聚合物,芳杂环聚合物等 |
芳香族 |
提高聚酯,聚酰胺分子量 |
常见聚合物
自由基聚合
有机玻璃(聚甲基丙烯酸甲酯)隐形眼睛材料(聚甲基丙烯酸羟乙酯)
聚醋酸乙烯酯(建筑粘合剂)
加聚和合连锁反应
三类单体
- 碳碳双键单烯类,共轭双烯类
- 羟基化合物
- 杂环化合物
条件
- 热力学:单体和聚合物的自由焓差小于零
- 动力学:有适当的引发剂,温度等动力学
三个基元反应
活性中心(reactive center)
-
可以是自由基,阳离子,阴离子,通过进攻π键,形成单体活性种
-
活性中心不同可分为:自由基聚合,阳离子聚合,阴离子聚合
- 自由基聚合是通过物理作用,使单体分子活化为活性自由基(共价键均裂)
-
均裂:形成两个中性自由基
R⋅∣⋅R−>2R⋅
-
异裂:形成一个阴离子,一个阳离子
A∣⋅⋅B−>A++B−
决定因素:电子效应(诱导效应,共轭效应),空间位阻
-
诱导效应是由电负性引起的,针对吸–排电子能力大小来说的(诱导效应就是我要做生意,你把钱借给我,我自己做生意。)
-
共轭效应则是一个典型的“均匀”过程,也可以理解为电子分散过程(共轭效应就是我有一个生意,你拿钱来入股,我们一起做生意。)
-
共轭体系是能形成共轭π键的体系
单键=一个σ键(头碰头)双键=一个σ键(头碰头)+(一个)π键(肩并肩)三键=一个σ键(头碰头)zd+(两个相互垂直的)π键(肩并肩)四键=一个σ键(头碰头)+(两个相互垂直的)π键(肩并肩)+(一个)δ键
- 醛,酮,杂环不能自由基聚合
- 烯类单体自由基聚合,离子聚合(可均裂,可异裂)
- 供(推,给)电子基团,阳离子聚合,供电子较弱的,丙烯,丁烯只能合成低分子油状物
- 吸电子基团,阴离子聚合
- 共轭体系适用三种聚合
- 卤素原子,有诱导效应又有共轭效应,只能进行自由基聚合
阴离子聚合⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧NO2CN自由基聚合⎩⎪⎨⎪⎧COOCH3CH=CH2C6H5阳离子聚合⎩⎪⎨⎪⎧C6H5CH3OR
空间位阻效应(体积位置数量)
- 两基团吸电子能力弱,自由基聚合
- 两基团吸电子能力强,阴离子聚合
- 两基团供电子能力强,阳离子聚合
- 两基团一供一吸电子,自由基呼和
聚合热力学
H−焓,E−内能,S−熵,G−自由焓(自由能)H=E+pV=G+TSG=H−TSΔH=ΔE+pΔV=ΔG+TΔSΔG=ΔH=TΔSΔH<0,ΔS<0⎩⎪⎨⎪⎧ΔG<0 ,聚合自发进行ΔG=0 ,聚合,解聚处于平衡ΔG>0 ,解聚
影响单体聚合热的因素
取代基的位阻效应
单体键能↓,聚合物键能↓↓,ΔH↓
共轭效应和超共轭效应
单体键能↑,则ΔH↓
取代基的电负性
单体键能↓,使ΔH↑
氢键,溶剂化作用
单体键能↑,ΔH↓
ΔG=ΔH−TΔS临界温度, Tc=ΔSΔH
-
聚合反应必为放热反应(吸热为证,放热为负)
-
聚合热越大,聚合倾向也越大
-
测定方法
直接热量法,燃烧热法,热力学平衡法
由标准生成热估算
ΔH=ΔHf.p0−ΔHf,m0
由键能估算
键能:分子中化学键强度的一种量度
-
影响因素
| 因素 |
位阻 |
共轭 |
氢键和溶剂化效应 |
强电负性取代基 |
| 聚合热 |
降低 |
降低 |
降低 |
升高 |
平衡常数和平衡单体浓度关系:
Ke,平衡常数 [M]e,单体浓度Ke=kdpkp=[M]e1ΔG=ΔG⊖+RT lnKe=(ΔH⊖−TΔS⊖+RT lnKe) 平衡时ΔG=0平衡浓度 Te=ΔS⊖−Rln KeΔH⊖=ΔS⊖+R ln[M]eΔH⊖
单体浓度和温度关系:
ln[M]e=R1(TeΔH⊖−ΔS⊖)
自由基聚合机理
自由基的种类
自由基反应
-
加成反应
⋅R+CH2=CHX−−>R−CH2−C⋅H(X)
-
转移反应
⋅R+R′H−−>R−H+R′
-
偶合反应
R⋅+R′−−>R−R′
-
歧化反应
CH3C.(CH3)CN+CH3C.(CH3)CN−−>CH3CH(CH3)CN+CH3C(CN)=CH2
-
氧化反应
HO⋅+Fe2+−−>HO−+Fe3−
自由基的稳定性和活性
- 共轭效应和空间效应使自由基稳定
- 斥电子诱导效应使自由基稳定性降低
- 共轭效应和诱导效应矛盾时,共轭效应为主
- 电子效应和空间效应矛盾时,空间效应为主
- 带共轭取代基,稳定
- 带吸电子取代基,稳定
- 带推电子取代基,活泼
链引发反应(活化能最高)(initiation reaction)
链增长反应(Propagation)
*链转移(Chain transfer)
聚合过程中,增长链从其他分子夺去一个原子形成稳定,但是这个分子又成新的自由基
-
向溶剂或链转移剂转移
链自由基向溶剂分子转移,聚合度降低,聚合速率不变
-
向单体转移
链自由基将弧单体转移到单体上,聚合度降低,活性不减弱,故速率未降低
-
向大分子转移
链自由基夺去稳定了的大分子,形成大自由基,转化率高,聚合物浓度大
-
向引发剂转移(引发剂的有道分解)
链自由基向引发剂转移,自由基浓度不变,聚合分子量降低,引发剂效率下降
链终止反应(Termination)
-
偶合终止
两链子自由基的弧电子相互结合成共价键
特征:聚合度是链自由基重复单元数的两倍,引发剂引发的两端均有残基
-
歧化终止
一个链夺取了另一个链自由基相邻碳原子的氢原子(一个完成聚合,一个有双键)
特征:聚合度和链自由基重复单元数相等,只有一端是引发剂残基,一个饱和端,一个不饱和端(原因如上原理)
反应特征:活化能很低,8−21kJ/mol
|
链引发 |
链增长 |
链终止 |
| 活化能 |
kd=10-4~10-6s-1 |
kp=102~104L/(mol·s) |
kt=106~108 L/(mol·s) |
| 速率常数 |
105~150kJ/mol |
16~33kJ/mol |
8~21kJ/mol |
自由基聚合特征:慢引发,快增长,速终止
少量(0.01%~0.1%)阻聚剂可使自由基聚合反应终止
引发剂
分子结构上具有弱键,易分解产生自由基进而引发单体聚合的物质。
-
偶氮类引发剂
偶氮二异丁腈(AIBN)
使用温度:45~65,解离能105KJ/mol。油溶性
- 分解只形成一种自由基,无诱导分解
- 稳定,能单独保存
- 分解时有N2逸出
- 分解后形成异丁腈,自由基缺乏脱氧能力,不能作为接枝聚合引发剂
-
有机过氧类引发剂
弱过氧键(O-O),加热均裂成个自由基
过氧化二苯甲酰(BPO)(第一步分解为苯甲酰自由基,第二步分解成苯基自由基放出CO2)
分解温度:60~80,解离能:124KJ/mol
最简单的:过氧化氢 (活化能比较高,220KJ/mol,一般不做单独引发剂)
-
氢过氧化物:
叔丁基过氧化物
异丙基过氧化物
-
过氧化物:
过氧化二叔丁基
过氧化二异丙苯
-
无机过氧类引发剂
水溶性引发剂,乳液聚合,水溶液聚合
分解温度:6080,解离能:109140KJ/mol
过硫酸盐:
过硫酸甲(K2S2O8)过硫酸铵[(NH4)2S2O8]
-
氧化-还原引发反应体系
将有机或无机过氧化物和还原剂复合,组成氧化-还原引发体系
活化能低(4060KJ/mol),引发温度低(050),聚合速率大
-
水溶性氧化-还原引发体系
氧化剂:过氧化氢,过硫酸盐,氢过氧化物
还原剂:无机还原剂(Fe2+等)有机还原剂
-
油溶性氧化-还原引发体系
氧化剂:氢过氧化物,
还原剂:叔胺,硫醇
引发剂分解动力学
-
分解速率常数
一级反应
Rd≡dt−d[I]=kd[I] kd分解速率常数,单位s−1积分得: ln[I]0[I]=−kdt [I]0[I]=e−kdt [I]时间为t时的引发剂浓度,mol/L[I]0引发剂的起始浓度,mol/L
-
半衰期
t1/2=kdln2=kd0.693t1/2≥6h,低活性t1/2≤1h,高活性6h>t1/2>1h,中等活性
分解速率参数或半衰期越短,引发剂的活性越高
- 分解速率常数与温度的关系
Arrhenius经验公式kd=Ade−Ed/RTlnkd=lnAd−Ed/RTEd分解活化能;Ad频率因子,Ed为正值,温度升高,kd增大
引发剂效率
f=消耗的引发剂引发剂×100%
引发剂选择
- 本体,悬浮和溶液聚合:油溶性引发剂
- 乳液聚合和水溶液聚合:水溶性引发剂
- 高温低活性引发剂,低温高活性引发剂
其他引发反应
- 热引发聚合:不加引发剂,在热的作用下发生自身聚合
- 光引发聚合:紫外过的激发形成自由基引发单体聚合
- 辐射聚合:高能辐射线引发的单体聚合
聚合速率
Rp单位时间内单体消耗量或聚合物生成量Rp=−dtd[M]=dtd[P]C转化率C=[M]0Δ[M]=[M]0[M]0−[M]×100%<==>[M]=[M]0(1−C)Rp=−dtd[M]=[M]0dtdC
-
聚合速率测定方法
-
直接法
沉淀,蒸馏,分离,精制,干燥,称重
-
间接法
测比容,粘度,折光率,吸收光谱,(最常用膨胀计发)
自由基聚合微观动力学
kp1=kp2...=kpRp=kp[M][M⋅][M⋅]代表Σ[RMi⋅]即自由基RM⋅,RM2⋅....RMx⋅的总和
-
链终止
自由基消失速率Rt
-
偶合终止
Rtc=2ktc[M⋅]2一次终止消失两个自由基
-
歧化终止
Rtd=2ktd[M]2
终止总速率
Rt=−dtd[M⋅]=2Kt[M⋅]2
-
稳态假定
链引发和链终止在某一时刻达到平衡,Ri=Rt,构成动态平衡
Ri=Rt=2Kt[M⋅]2[M⋅]=(2KtRi)21Rp=Kp[M](2KtRi)21
-
聚合总速率
R=Kp[M][M⋅]聚合度很大 R=Kp[M](2KtRi)21
-
聚合总速率很大假定
聚合度很大,引发的单体远远少于消耗的单体,Rp>=Ri
Rp=Kp(KtfKD)21[I]21[M]
-
引发剂浓度偏移
-
1/2次方
双基终止-0.5级,单级终止-1级
双基终止:
Rp=A[I]21+B[I]
-
1次方
Rp=K[I]n[M]mn=0.5−1,m=1−1.5,有的可达2
温度对聚合速率的影响
遵循Arrhenius公式,温度升高,速率常数K增大,聚合速率上升,聚合度下降
k=Ae−RTEK=Kp(KtKd)21K=Ap(AtAd)21e−RT[(Ep−2Et)+2Ed]
自动加速现象
理论浓度下降速率降低,但是到一定转化率,聚合速率大幅度上升。
- 主要是因体系粘度系数增加引起(凝胶效应)
- 链终止反应受扩散控制所致
产生原因:
链自由基双基终止
- 链自由基的平移
- 链段重排,活性中心靠近
- 双基相互反应而使链终止
自动加速良溶剂出现少,非溶剂(沉淀剂)出现早且显著,不良溶剂介于两者之间
动力学链长
ν:活性中从引发阶段到终止消耗的单体数 无链转移:引发速率增长速率ν=RiRp=RtRp=2Kt[M⋅]Kp[M]当Ri=Rt时[M⋅]=(2ktRi)21引发剂引发时Ri=2fkd[I]
平均聚合度和链长
双基偶合终止,Xn=2ν歧化终止,Xn=ν两种都有,ν<Xn<2ν
自由基聚合时,增加引发剂提高聚合速率的措施,往往导致聚合度下降
分子量和链转移反应
自由基聚合体系中,若存在容易被夺去原子(氢或氯等)的物质时,容易发生链转移反应
产生的影响:自由基终止,聚合度下降;形成新的自由基,可以再引发体系中的单体分子反应继续练增长
对聚合度的影响
|
聚合度 |
| 提高单停浓度 |
增加 |
| 增大引发剂浓度 |
降低 |
| 加入链转移剂 |
降低 |
| 单体,引发剂,链转移剂 |
|
阻聚机理
概念:新自由基没有引发活性,聚合停止,表现为阻聚作用
阻聚剂:和链自由生成非自由基or不能引发聚合的低活性自由基使聚合停止的化合物
缓聚剂:时使聚合速率减慢的化合物
诱导期:从引发剂开始分解到单体开始转化存在一个时间间隔
阻聚剂分类:
- 按组成
- 分子型阻聚剂:苯醌(能终止两个自由基),硝基化合物,芳胺
- 自由基型阻聚剂:DPPH
- 按自由基反应机理
- 加成型阻聚剂:与链自由基快速加成,转化为活性低的自由基
- 链转移型阻聚剂
- 电荷转移型阻聚剂
自由基共聚
共聚主要包括:自由基共聚,离子共聚
二元共聚:无规,交替,嵌段,接枝
等活性理论:自由基活性与链长无关
共聚物聚合度很大:链引发和链终止对共聚物组成的影响可以忽略
稳态:自由基总浓度和两种自由基的浓度都不变
无前末端效应:自由基活性仅决定于末端单体单元结构,于前末端单元的结构无关
无解聚反应:不可逆聚合
二元共聚物涉及两种单体,有两种链引发,四种链增长,三种链终止
链引发:R⋅+M1−>RM1⋅ Ri,1R⋅+M2−>RM2⋅ Ri,2链增长:M1⋅+M1−>M1⋅ R11=K11[M1⋅][M1]M1⋅+M2−>M2⋅ R12=K12[M1⋅][M2]M2⋅+M1−>M1⋅ R21=K21[M2⋅][M1]M2⋅+M2−>M2⋅ R22=K22[M2⋅][M2]链终止:M1⋅+M1⋅−>大分子 Rt11=K11[M1⋅]2M1⋅+M2⋅−>大分子 Rt12=K12[M1⋅][M2⋅]M2⋅+M2⋅−>大分子 Rt22=K22[M2⋅]2
摩尔分率F
f1=[M1]+[M2][M1] f1+f2=1F1=d[M1]+d[M2]d[M1]=r1f12+2f1f2+r2f22r1f12+f1f2
p共聚物组成与链引发,链终止无关
p共聚物自称通常不等于原料单体组成
p共聚物组成微分方程自适用于低化率
p共聚物引入竟聚率,r1=k11/k12;r2=k22/k21;
聚合方法
自由基聚合方法⎩⎪⎪⎪⎨⎪⎪⎪⎧本体聚合=>单体本身加少量引发剂(或不加)的聚合溶液聚合=>单体和引发剂溶于适当引发剂中的聚合悬浮聚合=>单体以液滴状悬浮在水中的聚合乳液聚合=>单体,水,水溶性引发剂,乳化剂配成乳液状态进行的聚合逐步聚合方法⎩⎪⎪⎪⎨⎪⎪⎪⎧熔融缩聚溶液缩聚界面缩聚固相缩聚=>固体单体在熔点以下发生聚合反应,或在形成聚合物的熔融温度以下进行聚合反应离子和配位聚合方法⎩⎪⎨⎪⎧溶液聚合淤浆聚合气相聚合=>合只有极少稀释剂或溶剂作催化剂的分散介质,并在单体沸点以上的温度下进行聚合。
均相体系
单体,引发剂和形成的聚合物均能完全溶解在反应介质,引发剂和聚合物均溶于单体的本体聚合或熔融缩聚反应,整个聚合体系适中为均相的反应。大多数本体聚合和溶液聚合
非均相体系
单体或聚合物不溶于介质,反应体系存在多相,例如悬浮聚合和乳液聚合
本体聚合
不加其他介质,只有单体本身,在少量引发剂,热,光等作用下进行聚合梵音
单体:气液固态单体
引发剂:油溶性
助剂:色料,增塑剂,润滑剂,抗氧剂
聚合场所:本体
优点:产品纯净,不存在介质分离问题,制作透明板材,可以连续或间歇生产
缺点:体系很粘稠,聚合热不易扩散,温度难控制,可以通过分段聚合解决
溶液聚合
将单体和引发剂溶于适当溶剂中进行的聚合反应。
优点:散热控温容易,可避免局部过热,体系粘度低,能消除凝胶效应
缺点:溶剂回收麻烦,设备利用率低聚合速率慢,分子量低
用途:涂料,胶粘剂
溶剂对聚合活性的影响:
溶剂对凝胶效应的影响:
- 好的溶剂,可以消除凝胶效应
- 沉淀剂,凝胶效应明显
- 劣溶剂,两者之间
悬浮聚合
将不溶于水的单体以小液滴悬浮在水中进行聚合。
单体液滴=>聚合物单体粘性粒子=>聚合物固体粒子
聚合场所:单体液滴
组成:单体,引发剂,水
分散剂:一类能将油溶剂单体分散在水中形成稳定悬浮液的物质
优点:
- 体系粘度低,分子量分布稳定
- 产品分子量比溶液聚合高,杂质含量比乳液聚合少
- 后处理工序比乳液聚合和溶液聚合简单生产成本低
缺点:
乳液聚合
单体在乳化剂作用和机械搅拌下,在水中分散成乳
单体:一般为油性单体
引发剂:水溶性或组分为水溶剂的引发剂
水:无粒子水
优点:
- 水做分散介质,传热控温容易
- 可在低温下聚合
- 可直接用于聚合物乳胶的场合 ,乳胶漆,胶粘剂等
缺点:
- 要得到固体聚合物,后处理麻烦成本高
- 难以除尽乳化剂残留物,对性能有影响
特点:聚合速率和分子量同时提高
乳化剂:
定义:一类可互不相容的油和水转变成难以分层的乳液的物质,属于表面活性剂
结构:分子通常又两部分组成亲水基团亲油非极性基团
乳化剂作用:使互不相容的油,水转变成相当稳定难以分层的乳液的过程。在较高浓度聚集成胶束
- 降低界面张力,使单体分散成细小的液滴
- 液滴保护层,防止聚集,使乳液更稳定,
- 形成胶束使单体增溶
ss




